Practice Problems Using Rolles Theorem and Mean Value Theorem

Explain why Rolle’s theorem is not applicable to the following functions in the respective intervals.

Problem 1 :

 f(x)  =  |(1/x)|, x ∊ [-1, 1]          Solution

Problem 2 :

f (x) = tan x, x ∊ [0, π]       Solution

Problem 3 :

f(x)  =  x - 2 log x, x ∊ [2, 7]            Solution

For each problem, determine if the Rolle's Theorem can be applied. If it can, find all values of c that satisfy the theorem. If it cannot, explain why not

Problem 4 :

y = (-x² + 1)/3x   [1, 6]

Solution

Problem 5 :

y = (x² - x - 12)/(x + 4)   [-3, 4]

Solution

Problem 6 :

y = (-x² - 2x + 8)/(-x + 3);   [-4, 2]

Solution

Using the Rolle’s theorem, determine the values of x at which the tangent is parallel to the x -axis for the following functions :

Problem 1 :

f(x)  =  x² − x, x ∈ [0, 1]

Solution

Problem 2 :

f(x)  =  (x² - 2x)/(x + 2), x ∈ [-1, 6]

Solution

Problem 3 :

f(x)  =   √x - (x/3), x ∈ [0, 9]

Solution

For each problem, find the values of c that satisfy Rolle's Theorem.

Problem 4 :

y = x² + 4x + 5; [−3, −1]

Solution

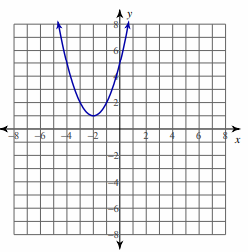
Problem 5 :

y = x³ - 2 x² - x - 1; [−1, 2]

Solution

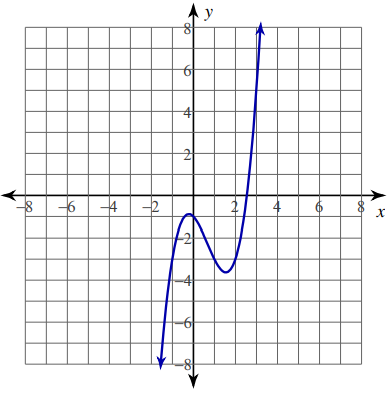
Problem 6 :

y = -2 sin (2x) [−π, π]

Solution

Problem 7 :

y = cos (2x) [π/3, 2π/3]

Solution

Problem 1 :

Explain why Lagrange’s mean value theorem is not applicable to the following functions in the respective intervals :

(i)  f(x)  =  (x+1)/x, x ∊ [-1, 2]          Solution

(ii)  f(x)  =  |3x+1|, x ∊ [-1, 3]         Solution

Problem 2 :

Using the Lagrange’s mean value theorem determine the values of x at which the tangent is parallel to the secant line at the end points of the given interval:

(i)  f (x)  =  x³ - 3x + 2, x ∊ [-2, 2]         Solution

(ii)  f(x)  =  (x-2)(x-7),  x ∊ [3, 11]        Solution

Problem 3 :

Show that the value in the conclusion of the mean value theorem for

(i) f (x) = 1/x

on a closed interval of positive numbers [a, b] is √ab

Solution

(ii) f (x) = Ax² + Bx + C on any interval [a, b] is (a + b)/2

Solution

Problem 4 :

Determine whether

f(x) = cos x - sin x

satisfies the MVT on the interval [π/4, 5π/4] if it does, find all numbers c in (π/4, 5π/4) such that f'(c) = f(b) - f(a) / (b - a)

Solution

Decide whether mean value theorem applies. If it applies, find the value of x that satisfy the theorem. 

Problem 5 :

f(x) = (x + 3) / (x - 3); [-1, 4]

Solution

Problem 6 :

f(x) = (1/3)x³ + (1/3)x - 4/3; [-1, 2]

Solution

Problem 1 :

A race car driver is racing at 20th km. If his speed never exceeds 150 km/hr, what is the maximum distance he can cover in the next two hours.

Solution

Problem 2 :

Suppose that for a function f (x), 

f'(x) ≤ 1 for all 1 ≤ x ≤ 4. Show that f(4) − f(1) ≤ 3 .

Solution

Problem 3 :

Does there exist a differentiable function f(x) such that f(0) = −1, f(2) = 4 and f'(x) ≤ 2 for all x . Justify your answer.

Solution

Problem 4 :

Show that there lies a point on the curve

f(x)  =  x(x+3)e^π/2, -3 ≤  x ≤ 0,

where the tangent is parallel to the x-axis.

Solution

Problem 5 :

Using mean value theorem prove that for a > 0, b > 0,

|e^-a-e^-b| < |a-b|

Solution

Problem 6 :

Skater Sully is riding a skateboard back and forth on a street that runs north/south. The twice differentiable function S model's Sully's position on a street, measured by how many meters north he is from his starting point at time t, measured in seconds from the start of his ride. The table below gives values of S(t) at selected times t.

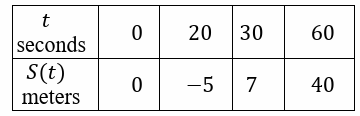
a) For 0 ≤ t ≤ 20must be there a time when Sully is 2 meters south of his starting point ? Justify your answer.

a) For 30 ≤ t ≤ 60 must be there a time t when Sully velocity 1.1 meters per pound  is 2 meters south of his starting point ? Justify your answer.

Solution

Problem 6 :

A particle is moving along the 𝑥-axis. The twice-differentiable function 𝑠 models the particles distance from the origin, measured in centimeters, at time 𝑡, measured in seconds.

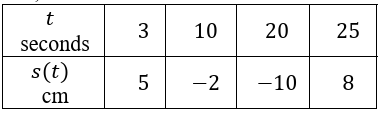
a. For 20 ≤ 𝑡 ≤ 25, must there be a time 𝑡 when the particle is at the origin? Justify your answer.

b. For 3 ≤ 𝑡 ≤ 10, must there be a time 𝑡 when the particle’s velocity is 1 cm per second? Justify your answer.

Solution

Problem 7 :

A hot air balloon is launched into the air with a human pilot. The twice-differentiable function ℎ models the balloon’s height, measured in feet, at time 𝑡, measured in minutes. The table below gives values of ℎ𝑡 at selected times 𝑡.

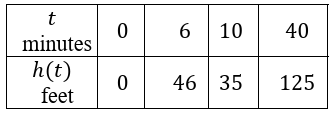
a)  For 6 ≤ 𝑡 ≤ 10, must there be a time 𝑡 when the balloon is 50 feet in the air? Justify your answer.

b)   For 10 𝑡 40, must there be a time 𝑡 when the balloon’s velocity is 3 feet per second? Justify your answer.

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.