PRACTICE QUESTIONS IN SLOPE AND EQUATION OF LINES

Problem 1 :

Find the slope of the line that passes through the points (2, 4) and (6, 12)

Solution :

Using the slope formula :

Slope  =  (y₂ – y₁)/(x₂ – x₁)

(2, 4)----->(x₁, y₁)

(6, 12)----->(x₂, y₂)

  =  (12 – 4)/(6 – 2)

  =  8/4

Slope  =  2

So, the slope is 2.

Problem 2 :

Find the slope of the line.

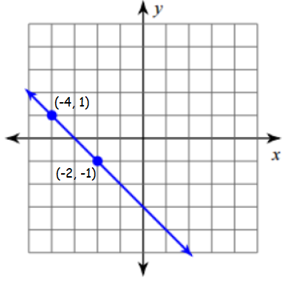
Solution :

In the given graph, the line passes through the points (-4, 1) and (-2, -1)

Using the slope formula :

Slope  =  (y₂ – y₁)/(x₂ – x₁)

(-4, 1)----->(x₁, y₁) and (-2, -1)----->(x₂, y₂)

  =  (-1 – 1)/(-2 + 4)

  =  -2/2

Slope  =  -1

So, the slope is -1.

Problem 3 :

A climber is on a hike. After 2 hours he is at an altitude of 400 feet. After 6 hours, he is at an altitude of 700 feet. What is the average rate of changes ?

Solution :

Let, x  =  time, y  =  altitude

Then, we have the points (2, 400) and (6, 700)

We are using slope formula to find the rate of changes.

Slope formula :

Slope  =  (y₂ – y₁)/(x₂ – x₁)

(2, 400)----->(x₁, y₁)

(6, 700)----->(x₂, y₂)

  =  (700 – 400)/(6 - 2)

  =  300/4

Slope  =  75

So, the slope is 75.

Problem 4 :

At what rate did the rainfall ?

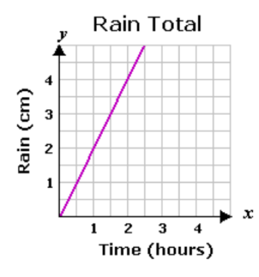
Solution :

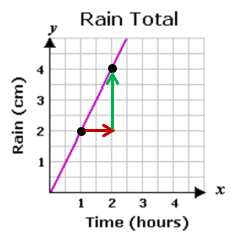
By observing the graph, the above line is a rising line. So, it will have a positive slope.

For the above line,

Rise  =  4

Run  =  2

Then,

Slope  =  Rise/Run

=  4/2

Slope  =  2

So, the answer is 2cm per hour.

Problem 5 :

Slope of parallel lines have _____________ slope.

Solution :

So, the slope of parallel lines is the same.

Problem 6 :

Write the equation of the line

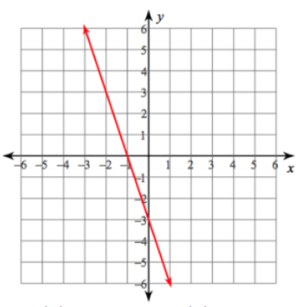
Solution :

By observing the graph, the above line is a falling line.

Slope  =  Rise/Run

=  - 3/1

Slope(m)  =  -3

Here y-intercept(b)  =  -3

Using slope-intercept form :

y  =  mx + b

y  =  -3x - 3

So, the equation of the line is y  =  -3x – 3.

Problem 7 :

y  =  3x + 2 and y  =  3x – 3

These lines are

(a) Parallel   (b) Perpendicular   (c) Neither

Solution  :

Given two lines have the same slope.

So, these lines are parallel.

Problem 8  :

Write an equation for a line parallel to the line

y  =  1/3x – 4 through (-3, 2)

Solution  :

Given, equation of the line y  =  1/3x – 4 and point (-3, 2)

Here slope(m)  =  1/3

Using point-slope form :

y – y₁  =  m(x – x₁)

(-3, 2)----->(x₁, y₁)

y – 2  =  1/3(x + 3)

y – 2  =  1/3x + 1

y  =  1/3x + 1 + 2

y  =  1/3x + 3 -----(2)

So, the equation of the line is y  =  1/3x + 3

Problem 9  :

Write an equation for a line parallel to the line

y  =  5/4x + 4 through (-4, -3)

Solution  :

Given, equation of the line y  =  5/4x + 4 and Point (-4, -3)

Here slope(m)  =  5/4

Using point-slope form :

y – y₁  =  m(x – x₁)

(-4, -3)----->(x₁, y₁)

y + 3  =  5/4(x + 4)

y + 3  =  5/4x + 5

y  =  5/4x + 5 - 3

y  =  5/4x + 2 -----(2)

So, the equation of the line is y  =  5/4x + 2.

Problem 10 :

Find the slope of the line.

Solution :

Rise  =  5 units and Run  =  3 units.

Slope  =  Rise / Run

Slope  =  5/3

Problem 11 :

Find the slope of the line.

Solution :

By observing the graph, the above line is a falling line.

Using rise over run formula :

For the above line,

Rise  =  5

Run  =  5

Slope  =  Rise/Run

Slope  =  - 5/5

Slope  =  -1

So, the answer is -1.

Problem 12 :

Find the slope of the line through each pair of points.

(-20, 13), (-15, 8)

Solution :

Given points, (-20, 13), (-15, 8)

Using the slope formula :

Slope  =  (y₂ – y₁)/(x₂ – x₁)

(-20, 13)----->(x₁, y₁)

(-15, 8)----->(x₂, y₂)

  =  (8 – 13)/(-15 + 20)

  =  -5/5

Slope  =  -1

So, the slope is -1.

Problem 13 :

Find the slope of the line through each pair of points.

(4, -1), (0, -16)

Solution :

Given points, (4, -1), (0, -16)

Using the slope formula :

Slope  =  (y₂ – y₁)/(x₂ – x₁)

(4, -1)----->(x₁, y₁)

(0, -16)----->(x₂, y₂)

  =  (-16 + 1)/(0 - 4)

  =  15/4

So, the slope is 15/4.

Problem 14  :

Write the point-slope form of the equation of the line passes through (-5, 5), parallel to y  =  -7/5x + 1

Solution :

Given point, (-5, 5) and parallel line y  =  -7/5x + 1.

Here slope(m)  =  -7/5

Using point-slope form :

y – y₁  =  m(x – x₁)

(-5, 5)----->(x₁, y₁)

y – 5  =  -7/5(x + 5)

So, the answer is y – 5  =  -7/5(x + 5).

Problem 15 :

Write the point-slope form of the equation of the line passes through (4, 1), parallel to y  =  1/2x - 4

Solution :

Given point, (4, 1) and parallel line y  =  1/2x – 4

Here slope(m)  =  1/2

Using point-slope form :

y – y₁  =  m(x – x₁)

(4, 1)----->(x₁, y₁)

y – 1  =  1/2(x + 4)

So, the answer is y – 1  =  1/2(x + 4).

Problem 16 :

Write the point-slope form of the equation of the line passes through (1, 2), perpendicular to y  =  -6/7x + 4

Solution :

Given point, (1, 2) and perpendicular line y  =  -6/7x + 4

slope(m)  =  -6/7

perpendicular slope  =  -1/m

=  -1/(-6/7)

  =  7/6

Using point-slope form :

y – y₁  =  m(x – x₁)

(1, 2)----->(x₁, y₁)

y – 2  =  7/6(x - 1)

So, the answer is y – 2  =  7/6(x - 1).

Problem 17 :

Write the point-slope form of the equation of the line passes through (-3, 5), perpendicular to y  =  1/3x + 4

Solution :

Given point, (-3, 5) and perpendicular line y  =  1/3x + 4

slope(m)  =  1/3

perpendicular slope  =  -1/m

=  -1/(1/3)

=  -3

Using point-slope form :

y – y₁  =  m(x – x₁)

(-3, 5)----->(x₁, y₁)

y – 5  =  -3(x + 3)

So, the answer is y – 5  =  -3(x + 3)

Problem 18 :

A radio station is giving away 22 Taylor Swift concert tickets every hour today. The radio station has a total of 528 tickets to give away. Write an equation in standard form that expresses the number of tickets left to give away at the radio station, y , as a function of the number of hours past, x.

a)  22x + 7y = 126       b) 22x + y = 528

c) 22x - y = 528         d) 22x - y = -176

Solution :

Number of hours = x

number of tickets left to give away at the radio station = y

Total number of tickets = 528

22x + y = 528

The graph to the right shows a line of best fit for data collected on the amounts of cell phone bills in relation to the number of minutes used. What is the equation of the line of best fit?

Solution :

By observing the graph, the y-intercept = 15

Two points on the line (200, 20) and (800, 35)

Slope = (35 - 20) / (800 - 200)

= 15/600

= 3/120

= 1/40

Writing the equation in slope intercept form, we get

y = (1/40)x + 15

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.