PRACTICE QUESTIONS OF GEOMETRY FOR SAT

Question 1 :

If the measure of angle A of triangle ABC is 3x, the measure of angle B is 5x and the measure of angle C is 4x, what is the value of x?

a) 12   b) 15   c) 20   d) 30   e) 45

Solution :

In a triangle, sum of interior of a triangle is 180.

<A + <B + <C  =  180

3x+4x+5x  =  180

12x  =  180

x  =  180/12

x  =  15

Question 2 :

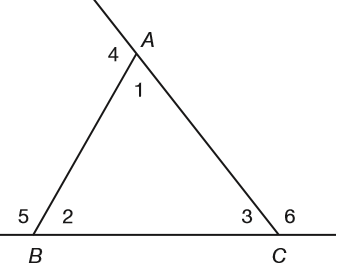
Which of the following number sentences is NOT true?

a) angle 1 + angle 2 = angle 5

b) angle 4 + angle 1 = angle 3 + angle 6

c) angle 3 + angle 2 = angle 4

d) angle 1 + angle 2 + angle 3 = 180

e) angle 4 + angle 5 + angle 6 = 360

Solution :

Option (a) is incorrect.

Problem 3 :

If the circle inscribed in square ABCD has a radius of r, what is the size of the shaded area in terms of r?

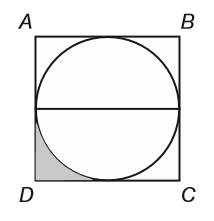
a) r² – πr²   b)  2r – πr²   c) 2r – π r²/4 

d) r² – (πr²/4)   e) (r² – πr²)/4 

Solution :

Required area

=  (Area of half of the square - area of semicircle)/2 

=  [a²/2 - (πr²/2)]/2

Here a  =  2r

=  [(2r)²/2 - (πr²/2)]/2

=  [2r² - (πr²/2)]/2

=  r² - (πr²/4)

Problem 4 :

The figure is an equilateral inscribed in  a circle with radius 10. 

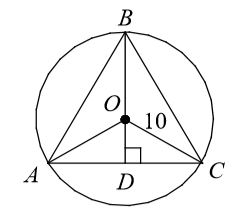
What is the measure of ∠AOC? 

Solution :

<AOB  =  <AOC  =  <COB

<AOC  =  (1/3) ⋅ 360

<AOC  =  120

Problem 5 :

What is the area of the isosceles trapezoid above? 

   A)  238       B)  252       C)  276       D)  308 

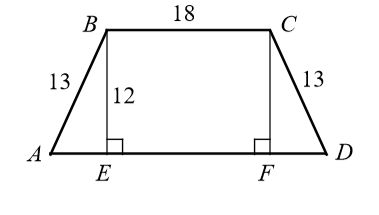
Solution :

Since BE is perpendicular to AD, triangle ABE is a right triangle.

AB²  =  AE² + EB²

13²  =  AE² + 12²

169- 144  =  AE²

AE  =  √25

AE  =  5

FD  =  5

AD  =  5+18+5

AD  =  28

Area of trapezoid  =  (1/2)⋅h (a+b)

=  (1/2)⋅12 (18+28)

=  6(18+28)

=  276

Problem 6 :

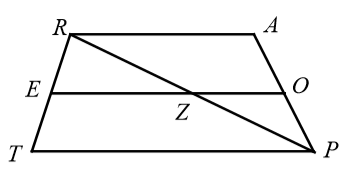
In the figure above, EO is the midsegment of trapezoid TRAP and RP intersect EO at point Z. If 15 = RA and 18 =EO, what is the length of EZ 

Solution :

The length of the midsegment of a trapezoid is average of lengths of bases.

EO  =  (1/2)(RA + TP)

18  =  (1/2)(15 + TP)

36  =  15 + TP

TP  =  36 - 15

TP  =  21

EZ  = (1/2)(21)

EZ  =  10.5

Problem 7 :

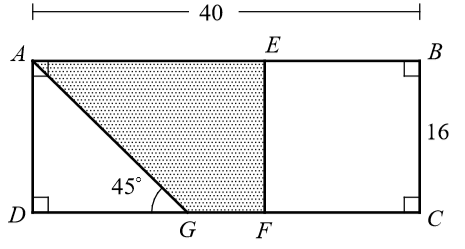
In the figure above, ABCD is a rectangle and BCFE is a square. If AB  =  40, BC  =  16 and <AGD = 45, what is the area of the shaded region? 

Solution :

Triangle ADG is special 45-45-90 right triangle.

FC  =  16

DF  =  DC - FC

DF  =  40-16

DF  =  24  =  AE

BC  =  AD  =  16  =  DG

GF  =  DF - DG

GF  =  24 - 16

GF  =  8

Area of the shaded region is in the form of trapezoid.

Area of trapezoid  =  (1/2)⋅h (a+b)

=  (1/2) 16 (24+8)

=  8 (32)

=  256

Problem 8 :

In a figure below, the radius of circle B is one third the radius of circle A. The shaded area is 128 π. What is the length of AB.

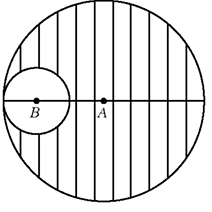
Solution :

Let R be the radius of the circle with center A

Let r be the radius of circle with center B.

Radius of circle B  = 1/3 of R

Area of shaded region

= Area of large circle - area of smaller circle

= πR² - π [(1/3) R]²

πR² - π [(1/3) R]² = 128 π

R² - (1/9) R² = 128

R² (8/9) = 128

R² = 128 x (9/8)

R² = 144

R = 12

r = 12/3 ==> 4

AB = 12 - 4

= 8

So, the length of AB is 8 cm.

Problem 9 :

In the figure given below, <B and <ACD are right angles, If AB = 8, BC = 6 and CD = 4, what is the length of AD ?

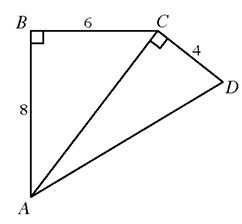
Solution :

In the picture above, we see two right triangles, they are triangle ABC and triangle ACD.

AC² = AB² + BC²

AC² = 8² + 6²

AC² = 64 + 36

AC² = 100

AC = 10

In triangle ACD,

AD² = AC² + CD²

AD² = 10² + 4²

= 100 + 44

AD² = 144

AD = 12

So, length of AD is 12 cm.

Problem 10 :

The base of a suitcase is 22 inches long and 18 inches wide. If umbrellas come in integer lengths only, what is the longest umbrella that will fit flat on the base of the suitcase?

Solution :

Find the greatest common divisor (GCD) of 22 and 18

GCD(22, 18) = 2

Divide the dimensions by the GCD to get the longest umbrella

22/2 = 11 inches, 18/2 = 9 inches

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.