PRACTICE QUESTIONS ON CIRCLES AND CYCLIC QUADRILATERALS

Question 1 :

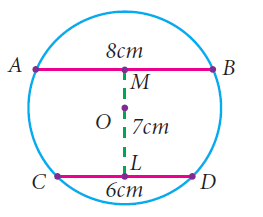
In the given figure, AB and CD are the parallel chords of a circle with centre O. Such that AB = 8cm and CD = 6cm. If OM ⊥ AB and OL ⊥ CD distance between LM is 7cm. Find the radius of the circle.

Solution :

Let us join the points OC, OD, OA and OB.

OA  =  OB  =  OC  and OD are equal in length and it is radius.

Let OL  =  x

In triangle OLD, 

CL  =  CD  =  3 cm

OL² + LD²  =  OD²

x² + 3²  =  OD²

OD²  =  x² + 9  ------------(1)

In triangle OAB, 

OM  =  7 - x

AM  =  BM  =  4 cm

OM² + MB²  =  OB²

(7 - x)² + 4²  =  OB²

OB²  =  (7-x)² + 16  ------------(2)

(1)  =  (2)

 (7-x)² + 16  =  x² + 9 

49 - 14x + x² + 16 - x² - 9  =  0

-14x + 56  =  0

x  =  56/14  =  4

By applying the value of x in (1), we get

OD²  =  4² + 9  

OD²  =  16 + 9  =  25

OD  =  5 cm

Question 2 :

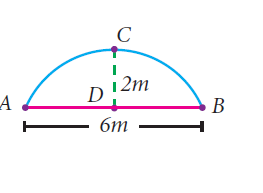
The arch of a bridge has dimensions as shown, where the arch measure 2 m at its highest point and its width is 6 m. What is the radius of the circle that contains the arch?

Solution :

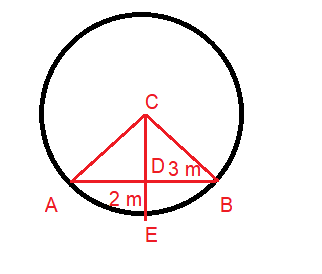
DB  =  2 m and DB  =  3 m

CE  =  CB  =  AC  (radius)

Let DC  =  x

In triangle CDB, 

CB²  =  CD² + DB²

CB²  =  x² + 3²  ---(1)

CE  =  x + 2

By applying the value of CE  =  x + 2 (CB) in (1), we get

(x + 2)²  =  x² + 9

x² + 4x + 4 - x² - 9  =  0

4x - 5  =  0

x  =  5/4

x  =  1.25

CE  =  1.25 + 2  =  3.25 m

Question 3 :

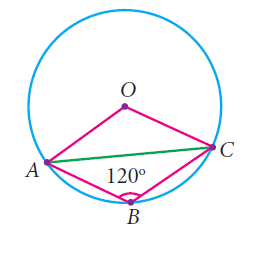
In figure, <ABC =120 , where A,B and C are points on the circle with centre O. Find <OAC ?

Solution :

Question 4 :

A school wants to conduct tree plantation programme. For this a teacher allotted a circle of radius 6m ground to nineth standard students for planting sapplings. Four students plant trees at the points A,B,C and D as shown in figure. Here AB = 8m, CD = 10m and AB is perpendicular to CD. If another student places a flower pot at the point P, the intersection of AB and CD, then find the distance from the centre to P.

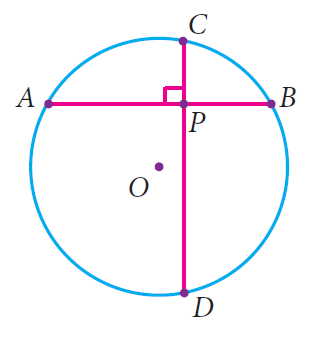
Solution :

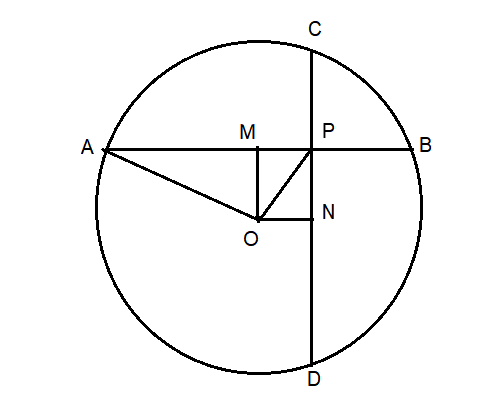
AM  =  (1/2) AB  

AM  =  (1/2)8  =  4

CN  =  (1/2) 10  =  5

OA  =  6

OA²  =  OM² + MO²

6²  =  OM² + 4²

36 - 16  =  OM²

OM  =  √20  =  2√5

OD²  =  ON² + ND²

6²  =  ON² + 5²

36 - 25  =  ON²

ON  =  √11

OMPN is a rectangle and OP is a diagonal.

OP²  =  ON² + PN²

OP²  =  √11² + (√20)²

OP²  =  11 + 20

OP  =  √31  =  5.56 (approximately)

Question 5 :

In the given figure, ∠POQ = 100° and ∠PQR = 30°, then find ∠RPO .

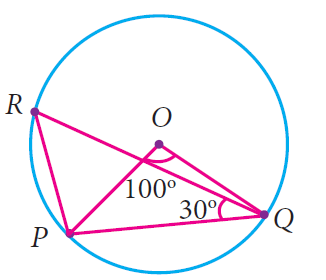
Solution :

By Inscribed Angle Theorem, 

∠PRQ  =  1/2 ⋅ m∠arc PQ

∠PRQ  =  1/2 ⋅ 100°

∠PRQ  =  50°

In ΔOPQ,

OP  =  OQ  =  Radius

So, ΔOPQ is an isosceles triangle. 

Because ∠POQ  =  100°, 

∠OPQ  =  ∠OQP  =  45°

In ΔPQR, 

∠RPQ + ∠PQR + ∠PRQ  =  180°

Substitute.

∠RPQ + 30° + 50°  =  180°

∠RPQ + 80°  =  180°

Subtract 80° from each side. 

∠RPQ  =  100°

∠RPO  =  ∠RPQ - ∠OPQ

∠RPO  =  100° - 45°

∠RPO  =  55°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.