PRACTICE QUESTIONS ON COORDINATE GEOMETRY FOR GRADE 10

Question 1 :

PQRS is a rectangle formed by joining the points P(-1,-1), Q(-1, 4), R(5, 4) and S(5,-1) . A, B, C and D are the mid-points of PQ, QR, RS and SP respectively. Is the quadrilateral ABCD a square, a rectangle or a rhombus? Justify your answer.

Solution :

Midpoint of the side PQ  =  A

Midpoint of the side QR  =  B

Midpoint of the side RS  =  C

Midpoint of the side SP  =  D

A = (x₁ + x₂)/2, (y₁ + y₂)/2

P(-1,-1), Q(-1, 4)

A  =  (-1 + (-1))/2, (-1 + 4)/2

 A  =  (-1, 3/2)

Q(-1, 4) R(5, 4)

B  =  (-1 + 5)/2, (4 + 4)/2

 B  =  (2, 4)

R(5, 4) and S(5,-1)

C  =  (5 + 5)/2, (4 + (-1))/2

 C  =  (5, 3/2)

S(5,-1) and P(-1,-1)

D  =  (5 + (-1))/2, (-1 + (-1))/2

 D  =  (2, -1)

Distance between AB  =  √(x₂ - x₁)² + (y₂ - y₁)²

Since the length of all sides are equal, it may be a square or rhombus not a rectangle.

I order to check if it is a square, let us find the slope of the sides AB and BC. If they are perpendicular, then it is square otherwise it is rhombus.

A (-1, 3/2) B (2, 4)

m₁  =  (y₂ - y₁)/(x₂ - x₁)

=  (4 - (3/2))/(2 + 1)

=  (5/2)/3

m₁  =  5/6 ----(1)

B(3, 4) C (5, 3/2)

m₂  =  ((3/2) - 4)/(5 - 3)

=  (-5/2)/2

m₂  =  -5/4 ----(2)

Since they are not perpendicular, it is not square. Hence it is rhombus.

Question 2 :

The area of a triangle is 5 sq.units. Two of its vertices are (2, 1) and (3, –2). The third vertex is (x, y) where y = x + 3 . Find the coordinates of the third vertex.

Solution :

Let the missing vertex be (x, y)

Area of triangle  =  5

A (2, 1) B (3, -2) and C (x, y)

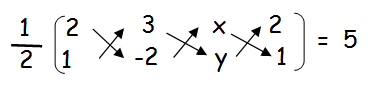
(1/2)[(-4 + 3y + x) - (3 - 2x + 2y)]  =  5

x + 3y - 4 - 3 + 2x - 2y  =  10

3x + y - 7  =  10

3x + y  =  17  -----(1)

y = x + 3 (Given)

By applying the value of y in (1), we get

3x + x + 3  =  17

4x  =  17 - 3

4x  =  14

x  =  7/2

By applying the value of x in the given equation, we get 

y  =  (7/2)  + 3

y = (7 + 6)/3

y = 13/3

Hence the third vertex is (7/2, 13/3)

Question 3 :

If the coordinates of points A and B are (–2, –2) and (2, –4) respectively, find the coordinates of the point P such that AP = (3/7) 𝐴𝐵, where P lies on the line segment AB.

Solution :

AP/AB = 3/7

AB = AP + PB

7 = 3 + PB

PB = 7 - 3

PB = 4

AP : PB = 3 : 4

To find the point which divides the line segment in the ratio m : n

A(–2, –2) and B(2, –4)

= [3(2) + 4(-2)]/(3 + 4), [3(-4) + 4(-2)]/(3 + 4)

= (6 - 8)/7, (-12 - 8)/7

= -2/7, -20/7

Question 4 :

If three consecutive vertices of a parallelogram ABCD are A(1, -2 ), B(3, 6) and C (5, 10), find its fourth vertex D.

Solution :

In a parallelogram, midpoint of the diagonals will be equal.

Let the fourth vertex be D(x, y)

Midpoint of diagonal AC = Midpoint of diagonal BD

midpoint = (x₁ + x₂)/2, (y₁ + y₂)/2

Midpoint of AC = (1 + 5)/2, (-2 + 10)/2

= 6/2, 8/2

= (3, 4) ------(1)

Midpoint of BD = (3 + x)/2, (6 + y)/2 ------(2)

So, the fourth vertices is (3, 2).

Question 5 :

In what ratio is the line segment joining the points A (-2,  -3) and B(3, 7) divided by the y-axis? Also, find the coordinates of the point of division

Solution :

When the point divides the y-axis, the value of x will be 0. The required point on the y-axis will be (0, y).

Let the required ratio be l : m

= (lx₂ + mx₁) / (l + m), (ly₂ + my₁) / (l + m)

l(3) + m(-2) / (l + m), l(7) + m(-3) / (l + m) = (0, y)

l(3) + m(-2) / (l + m) = 0

3l - 2m = 0

3l = 2m

l/m = 2/3

l : m = 2 : 3

Applying this ratio, we get

l(7) + m(-3) / (l + m) = (0, y)

[2(7) + 3(-3)] / (2 + 3) = y

14 - 9 / 5 = y

5/5 = y

y = 1

So, the required point on the y-axis is (0, 1).

Question 6 :

Points A (-1, y) and B(5, 7 ) lie on a circle with center O (2 , -3y ). Find the values of y. Hence, find the radius of the circle.

Solution :

Radius is the distance between center and point on the circle.

Distance between OC = distance between OB

 √(x₂ - x₁)² + (y₂ - y₁)²

√(2 + 1)² + (-3y- y)² = √(2 - 5)² + (-3y - 7)²

√3² + (-4y)² = √(-3)² + (-3y - 7)²

(-4y)² = (-3y - 7)²

16y² = 9y² + 42y + 49

16y² - 9y² - 42y - 49 = 0

7y² - 42y - 49 = 0

y² - 6y - 7 = 0

(y - 7)(y + 1) = 0

y = 7 and y = -1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.