PRACTICE QUESTIONS ON DIVISIBILITY RULES

Question 1 :

If the number 517*324 is completely divisible by 3, then the smallest whole number in the place of * will be ?

(A)  2     (B)  3    (C)  4    (D)  5

Solution :

Divisibility rule for 3 :

If the sum of all the digits of the given number is divisible by 3, then we decide that the given number is also divisible by 3.

Let "x" be the unknown, then 

  =  (5 + 1 + 7 + x + 3 + 2 + 4) / 3

  =  (22 + x) / 3

If x  =  2, then 22 + x will become 24 and it is divisible by 3.

Hence the smallest whole number for x should be 2.

Question 2 :

If the number 481*673 is completely divisible by 9, then the smallest whole number in the place of * will be ?

(A)  4     (B)  3    (C)  6    (D)  7

Solution :

Divisibility rule for 9 :

If the sum of all the digits of the given number is divisible by 9, then we decide that the given number is also divisible by 9.

  =  (4 + 8 + 1 + x + 6 + 7 + 3) / 9

  =  (29 + x) / 9

If x  =  7, then

  =  (29 + 7) / 9

  =  36/9

divisible by 9 

Hence the smallest whole number for x should be 7.

Question 3 :

How many three digit numbers are divisible by 5 or 9?

(A) 260   (B) 280   (C) 200   (D) 180

Solution :

To find the total number three digit numbers divisible by 5 or 9, let us use the trick given below.

  =  (Number of 3 digit numbers divisible by 5) +  (Number of 3 digit numbers divisible by 9) -  (Number of 3 digit numbers divisible both 5 and 9) 

3 digit numbers divisible by 5 :

100, 105, 110, .............., 995

The sequence is arithmetic progression. To find the number of terms, we use the formula

a_n  =  a + (n - 1) d

a  =  first term (100)

d  =  common difference (105 - 100  =  5)

a_n  =  n^th term (995)

995  =  100 + (n - 1) 5

895  =  5(n - 1)

n - 1  =  179

n  =  180

3 digit numbers divisible by 9 :

108, 117, 110, .............., 999

The sequence is arithmetic progression. To find the number of terms, we use the formula

a_n  =  a + (n - 1) d

a  =  108, d  =  9 and a_n  =  999

999  =  108 + (n - 1) 9

891  =  9(n - 1)

n - 1  =  99

n  =  100

3 digit numbers divisible by both 5 and 9 :

If the number is divisible by 45, then it is also divisible by both 5 and 9.

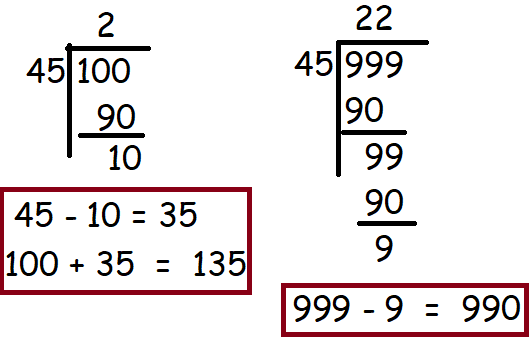
First three digit number divisible by 45 is 135.So the next term of the sequence will be increased by 45.

135, 180, ..........., 990

a_n  =  a + (n - 1) d

a  =  135, d  =  45 and a_n  =  990

990  =  135 + (n - 1) 45

990 - 135  =  45(n - 1)

45(n - 1)  =  855

n - 1  =  19

n  =  20

Number of 3 digit numbers divisible by 5  =  180

Number of 3 digit numbers divisible by 9  =  100

Number of 3 digit numbers divisible both 5 and 9  =  20

Number of three digit numbers divisible by 5 or 9 

  =  180 + 100 - 20

  =  260

Hence the number of three digit numbers divisible by both 5 and 9 is 260.

Question 4 :

If x and y are two digits of the number 653xy such that this number is divisible by 80, then x + y  =  ?

(A)  2     (B)  3    (C)  4    (D)  5

Solution :

Factors of 80 are 8 and 10. If the number is divisible by both 8 and 10, we can decide that the given number is divisible by 80.

If the unit digit of the given number is 0, then it is divisible by 10. To check if it is divisible by 8, we have to consider the last three digits of the number.

Let x = 2 and y = 0

Last three digits  =  320 (divisible by 8).

So, x + y  ==>  2 + 0  ==>  2

Hence the value of x + y is 2.

Question 5 :

On dividing a number by 357, we get 39 as remainder. On dividing the same number by 17, what will be the remainder ?

(A)  2     (B)  3    (C)  4    (D)  5

Solution :

Let "x" be the required number

Using division algorithm, 

Dividend  =  Divisor x quotient + Remainder

x  =  357 q₁ + 39  -----(1)

x  =  17 q₂ + r -----(2)

If q₁  =  1, then x  =  357(1) + 39

x  =  396

If we divide 396 by 17, we will get 5 as remainder.

(We will get the same remainder by applying all the values for q1).

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.