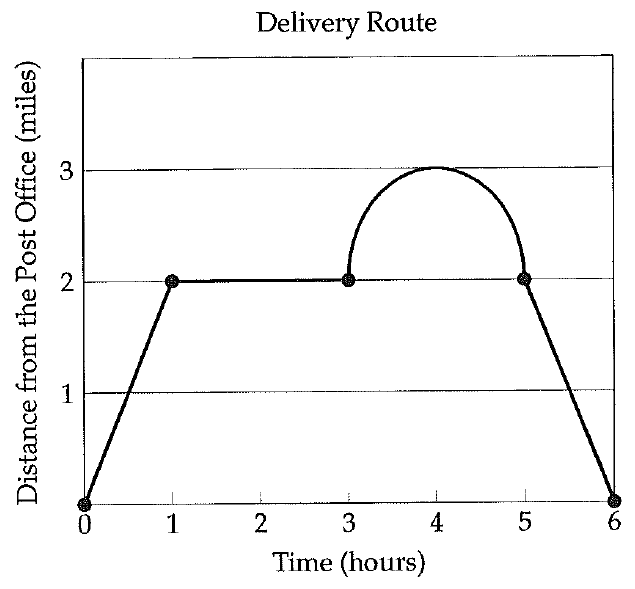
PRACTICE WORKSHEET RELATIONS AND FUNCTIONS WITH ANSWERS

Question 1 :

If the ordered pairs (x² − 3x, y² + 4y) and (-2,5) are equal, then find x and y.

Question 2 :

The Cartesian product A×A has 9 elements among which (–1, 0) and (0,1) are found. Find the set A and the remaining elements of A×A.

Question 3 :

Given that f(x)  =  

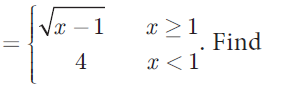
Question 4 :

Let A= {9, 10, 11, 12, 13, 14, 15, 16, 17} and let f : A-> N be defined by f (n) = the highest prime factor of n ∈ A. Write f as a set of ordered pairs and find the range of f.

Question 5 :

Two sets have m and k elements. If the total number of subsets of the first set is 112 more than that of the second set, find the values of m and k.

Question 6 :

If n(P(A)) = 1024, n(AUB) = 15 and n(P(B)) = 32, then find n(AnB)

Detailed Answer Key

Question 1 :

If the ordered pairs (x² − 3x, y² + 4y) and (-2,5) are equal, then find x and y.

Answer :

Question 2 :

The Cartesian product A×A has 9 elements among which (–1, 0) and (0,1) are found. Find the set A and the remaining elements of A×A.

Answer :

So, in this question since A X A has 9 elements, so the number of elements in the set  A must obviously be 3.

Since the given elements of the cross product have -1, 0 and 1 as part of the entries, clearly these only must be the elements of the set A.

So A = {-1, 0, 1}

A X A

  =  {(-1, -1),(-1, 0),(-1, 1),(0, -1),(0, 0),(0, 1),(1, -1),(1, 0),(1, 1)}

Question 3 :

Given that f(x)  =  

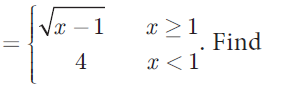
(i) f (0) (ii) f (3) (iii) f (a+1) in terms of a.(Given that a ≥  0)

Answer :

(i)  f(0)

Instead of x, we have 0, it is less than 1

f(0)  =  4

(ii)  f(3)

Instead of x, we have 3, it is greater than 1

f(3)  =  √(3 - 1)

f(3)  =  √2

(iii) f (a+1) 

Instead of x, we have a+1, it is greater than 1

f(a + 1)  =  √(a + 1 - 1)

f(a + 1)  =  √a

Question 4 :

Let A= {9, 10, 11, 12, 13, 14, 15, 16, 17} and let f : A-> N be defined by f (n) = the highest prime factor of n ∈ A. Write f as a set of ordered pairs and find the range of f.

Answer :

Set ordered pairs :

=  {(9,3) (10, 5)(11, 11)(12, 3)(13, 13) (14, 7) (15, 5) (16,2) (17, 17)}

Range  =  {2, 3, 5, 7,  11, 13, 17}

Question 5 :

Two sets have m and k elements. If the total number of subsets of the first set is 112 more than that of the second set, find the values of m and k.

Solution :

If a set contains n number of elements, then using the formula 2ⁿ, we find the number of subsets.

Number of subsets of a set containing m elements = 2^m

Number of subsets of a set containing k elements = 2^k

To find the more number of subsets in second set which is containing k elements, we have to find the difference between number of subsets in these two sets.

2^m - 2^k = 112

Factoring 2^k, we get

2^k (2^{m - k} - 1) = 112

Writing 112 in exponential form, we get

2^k (2^{m - k} - 1) = 2⁴ x 7

2^k = 2⁴

So, one of the possible value of k is 4. Then 2^{m - k} - 1 = 7

 2^{m - k} - 1 = 7

 2^{m - k}  = 8

 2^{m - k}  = 2³

m - k = 3

m - 4 = 3

Then m must be 7.

Question 6 :

If n(P(A)) = 1024, n(AUB) = 15 and n(P(B)) = 32, then find n(AnB)

Solution :

n(P(A)) = 1024 = 2¹⁰

Number of subsets = 2^m

Where m is the number of elements in the set A. So, number of elements in the set A is 10.

n(P(B)) = 32= 2⁵

Number of elements in set B is 5.

n(A) = 10, n(B) = 5 given that n(AUB) = 15

n(AUB) = n(A) + n(B) - n(AnB)

15 = 10 + 5 - n(AnB)

15 = 15 - n(AnB)

n(AnB) = 0

So, A and B are mutually exclusive sets.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.