PRE CALCULUS PROBLEMS AND SOLUTIONS
(Part - 5)

Problem 1 :

Joe invested $4500 at a fixed annual interest rate compounded annually. At the end of 12 years, the investment has doubled in value.

To the nearest hundredth of a percent, Joe’s investment pays interest at _____ %/year compounded annually.

Solution :

Problem 2 :

p(x) = 3x³ – 2x² – 19x – 6

In order to factor the polynomial function above, a student determined that the function has a zero of x = 3. He then wrote the polynomial as a product of a linear factor and a quadratic factor, as shown below, where a, b, and c ∈ I.

p(x) = (x + a)(3x² + bx + c)

Which of the following rows shows the correct values for a and b ?

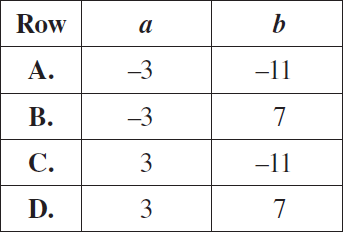
Solution :

Problem 3 :

A particular polynomial function has the following characteristics.

• A factor of (x + 2) with multiplicity 3
• P(0) = –24
• A minimum value of –66

For the polynomial function described above, the minimum possible degree is i and the leading coefficient is ii. The statement above is completed by the information in row

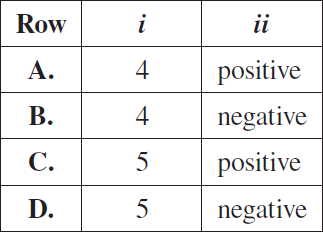
Solution :

Problem 4 :

The graph of the polynomial function, shown below, has integral x- and y-intercepts. The equation of the function can be written in the form

p(x) = ax⁴ + bx³ + cx² + dx + e,

where a, b, c, d, e ∈ I.

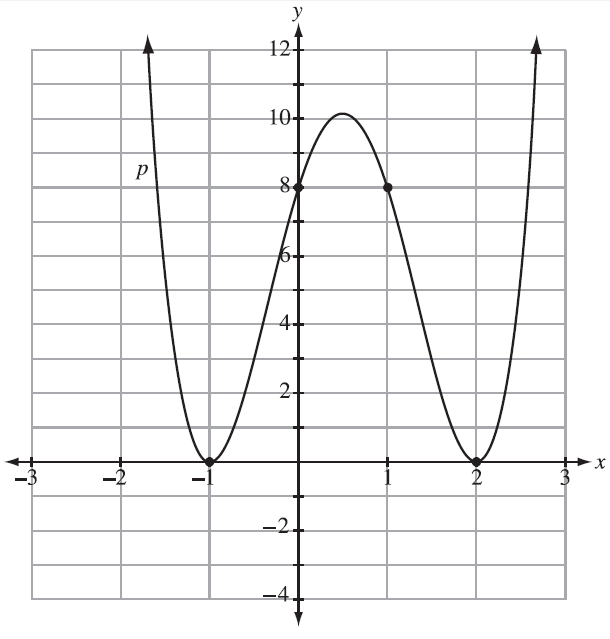
In the equation above, the values of a and e are, respectively, _____ and _____.

Solution :

Problem 5 :

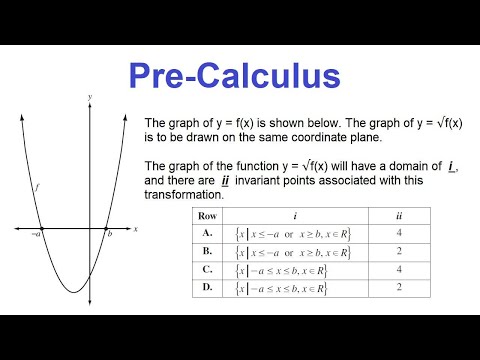
The graph of y = f(x) is shown below.

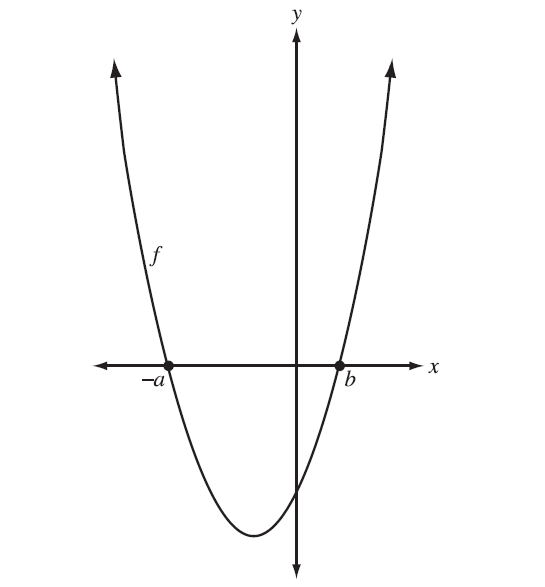
The graph of y = √f(x) is to be drawn on the same coordinate plane. The graph of the function y = √f(x) will have a domain of i , and there are ii invariant points associated with this transformation.

The statement above is completed by the information in row