PRECALCULUS OPTIMIZATION PROBLEMS WITH SOLUTIONS

Steps for Solving Optimization Problems

1) Read the problem.

2) Sketch a picture if possible and use variables for unknown quantities.

3) Write a function, expressing the quantity to be maximized or minimized as a function of one or more variables.

4) If your function has more than one variable, use information from the rest of the problem to solve for this variable in terms of the other

5) Determine the domain of the independent variable (the values for which the stated problem makes sense.)

6) Determine the maximum and minimum values by using your graphing calculator. Draw a sketch of the function you used, label your answer on your sketch, and then write your answer in a sentence.

Example Problems of Optimization

Example 1 :

An open box is to be made from a rectangular piece of cardstock, 8.5 inches wide and 11 inches tall, by cutting out squares of equal size from the four corners and bending up the sides. Find the maximum volume that the box can have. What size squares should be cut to create the box of maximum volume?

Solution :

Let x be the side length of square to cut out.

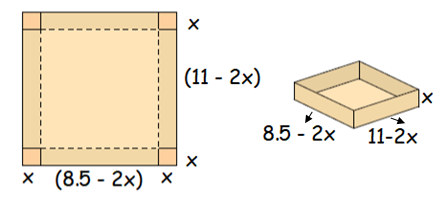
Volume of the box  =  length ⋅ width ⋅ height

  =   (8.5 - 2x) ⋅ (11 - 2x) ⋅ x

Domain of the function :

8.5 - 2x  =  0

2x  =  8.5

x  =  4.25

Domain is 0 < x < 4.25

Maximum value is 66.148. So the side length of square to cut out is 1.585 inches.

Example 2 :

A farmer has 120 feet of fencing with which to enclose two adjacent rectangular pens as shown. What dimensions should be used so that the enclosed area will be a maximum? What will the area be?

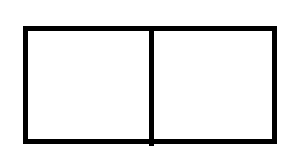
Solution :

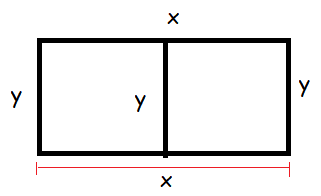
Let x and y be the length and width of the rectangular field respectively.

Length of fencing  =  120 feet

x + y + x + y + y  =  120

2x + 3y  =  120

3y  =  120 - 2x

y  =  (120 - 2x)/3

Area of the filed  =  length (width)

  =  x ⋅ [(120 - 2x)/3]

Domain of the function :

0 < x < 60

Using graphing calculator, we get

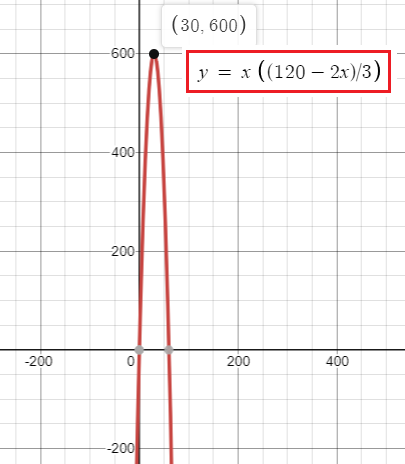
Maximum at x  =  30

Applying the value of y, we get

y  =  (120 - 60)/3

y  =  60/3

y  =  20

Area of the rectangular field  =  30(20)

  =  600 square feet

So, we get the maximum area enclosed by the dimension 30 feet and 20 feet. The maximum area is 600 square feet.

Example 3 :

A closed box with a square base must have a volume of 5000 cu. cm. Find the dimensions of the box that will minimize the amount of material used.

Solution :

Volume of the box with a square base  =  5000 cu.cm

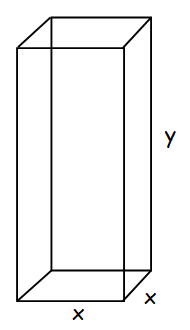
Let x be the length and width of the square base of cuboid and y be the height of cuboid.

Volume of cuboid  = length ⋅ width ⋅ height

  =  x ⋅ x ⋅ y

  =  x² y

x² y  =  5000

y  =  5000/x²

In order to find the material to be minimized, we should find the surface area of cuboid.

Surface area of closed cuboid box  =  2(lb + bh + hl)

  =  2(x² + xy + xy)

  =  2(x² + 2xy)

  =  2x² + 4xy

  =  2x² + 4x(5000/x²)

S(x)  =  2x² + (20000/x)

The volume of cuboid created by applying the material will not exceed 5000.

Domain is 0 < x < √5000

Using graphing calculator, we find

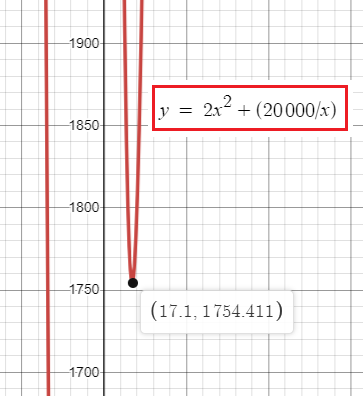
Side length of square base  =  17.1 cm

length of cuboid  =  17.1

Breadth of cuboid  =  17.1

Height of cuboid  (y)  =  5000/(17.1)²

  =  5000/292.41

  =  17.1

Hence the dimensions are 17.1 cm and 17.1 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.