PRECALCULUS PROBLEMS AND SOLUTIONS
(Part - 11)

Problem 1 :

You are given the dollar value of a product in 2015 and the rate at which the value of the product is expected to change during the next 5 years. Write a linear equation that gives the dollar value V(t) of the product in terms of the year t. (Let t = 15 represent 2015)

Solution :

Problem 2 :

The “rise to run” ratio of the roof of a house determines the steepness of the roof. The rise to run ratio of the roof in the figure is y = 2 to x = 3. Determine the maximum height in the attic of the house, if the house is w = 30 feet wide.

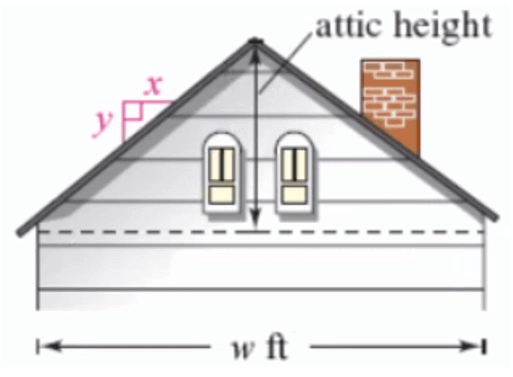
Solution :

Problem 3 :

Use the graphs of f and g to graph h(x) = (f + g)(x).

(To graph h(x), use 4 segments each with closed end points on both ends)

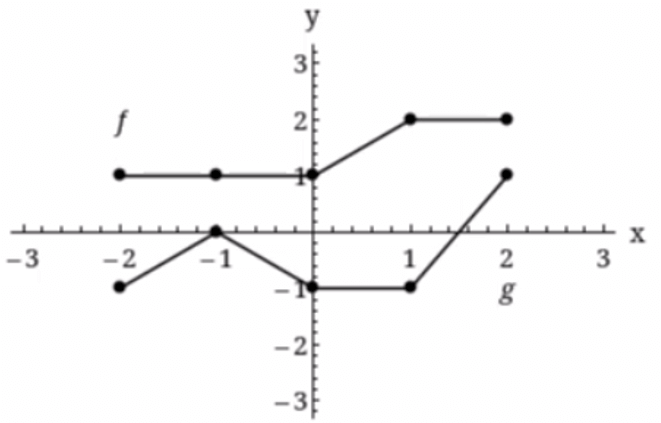
Solution :

Problem 4 :

Find the following. (Simplify your answers completely.)

a)  (f + g)(x)

b)  (f - g)(x)

c)  (fg)(x)

d)  (f/g)(x)

What is the domain of f/g? (Enter your answer using interval notation)

Solution :

Problem 5 :

f(x) = x² - 1

g(x) = x - 3

Evaluate the indicated function algebraically for f(x) and g(x) given  above.

Solution :

You might like these

Precalculus Problems and Solutions (Part - 1)

Precalculus Problems and Solutions (Part - 2)

Precalculus Problems and Solutions (Part - 3)

Precalculus Problems and Solutions (Part - 4)

Precalculus Problems and Solutions (Part - 5)

Precalculus Problems and Solutions (Part - 6)

Precalculus Problems and Solutions (Part - 7)

Precalculus Problems and Solutions (Part - 8)

Precalculus Problems and Solutions (Part - 9)

Precalculus Problems and Solutions (Part - 10)

Precalculus Problems and Solutions (Part - 11)

Precalculus Problems and Solutions (Part - 12)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.