PROBABILITY FOR ROLLING 2 DICE 

Rolling two dice always plays a key role in probability concept. Whenever we go through the stuff probability in statistics, we will definitely have examples with rolling two dice. 

Sample Space When 2 Dice are Rolled

Look at the six faced die which is given below. 

The above six faced die has the numbers 1, 2, 3, 4, 5, 6 on its faces. 

When a die is rolled once, the sample space is

S  =  {1, 2, 3, 4, 5, 6}

So, total no. of all possible outcomes  =  6 

When two dice are rolled, total no. of all possible outcomes

=  6 x 6

=  36

Here, the sample space is given when two dice are rolled 

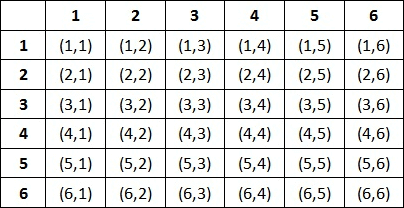
Let us understand the sample space of rolling two dice.

For example,

(4, 3) stands for getting '4' on  the first die and and '3' on the second die.

(1, 6) stands for getting '1' on  the first die and and '6' on the second die.

Probability for Rolling 2 Dice - Formula

We can use the formula from classic definition to find probability when two dice are rolled.

or

Since there are 36 outcomes in total when two dice are rolled, we have

n(S)  =  36

Solved Problems

Problem 1 :

A dice is rolled twice. What is the probability of getting a difference of 2 points?

Solution :

If an experiment results in p outcomes and if the experiment is repeated q times, then the total number of outcomes is pq.

In the present case, since a dice results in 6 outcomes and the dice is rolled twice, total no. of outcomes or elementary events is 62 or 36.

We assume that the dice is unbiased which ensures that all these 36 elementary events are equally likely.

Now a difference of 2 points in the uppermost faces of the dice thrown twice can occur in the following cases :

Thus denoting the event of getting a difference of 2 points by A, we find that the no. of outcomes favorable to A, from the above table, is 8.

By classical definition of probability, we get

P(A)  =  8/36

P(A)  =  2/9

Problem 2 :

Two dice are thrown simultaneously. Find the probability that the sum of points on the two dice would be 7 or more.

Solution :

If two dice are thrown then, as explained in the last problem, total no. of elementary events is 62 or 36.

Now a total of 7 or more i.e. 7 or 8 or 9 or 10 or 11 or 12 can occur only in the following combinations :

Sum  =  7 -----> (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)

Sum  =  8 -----> (2, 6), (3, 5), (4, 4), (5, 3), (6, 2)

Sum  =  9 -----> (3, 6), (4, 5), (5, 4), (6, 3)

Sum  =  10 -----> ((4, 6), (5, 5), (6, 4)

Sum  =  11 -----> (5, 6), (6, 5)

Sum  =  12 -----> (6, 6)

Thus the no. of favorable outcomes is 21.

Letting A stand for getting a total of 7 points or more, we have

P(A)  =  21/36

P(A)  =  7/12

Problem 3 :

Two dice are thrown simultaneously. Find the probability of getting a doublet. 

Solution :

Let us look at the sample when two dice are rolled. 

In the sample space of rolling two dice, there are six cases when in which doubles are rolled. 

They are 

(1, 1), (2, 2), (3, 3), (4, 4), (5, 5) and (6, 6)

Letting A stand for getting a doublet, we have

P(A)  =  6/36

P(A)  =  1/6

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.