PROBABILITY OF INDEPENDENT EVENTS

Let us consider the two events A and B. A is considered to be the first event and B as second event. 

Because A is the first event, it will not be influenced by the second event B. 

If the occurrence of the second event B is not influenced by the occurrence of the first event A, then B is known to be independent of A.

It also follows that in this case, A is also independent of B.

Therefore, A and B are known as mutually independent or just independent.

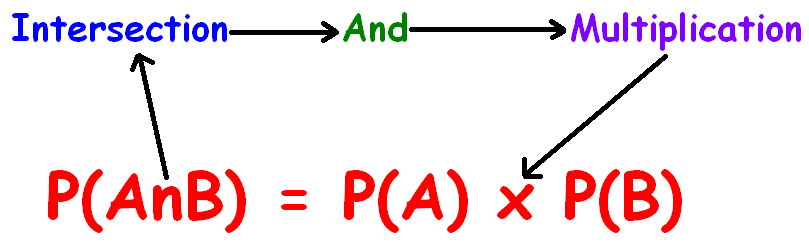
Then, joint Probability of the events A and B is denoted by P(AnB).

The formula to find P(AnB) is given by 

P(AnB)  =  P(A) x P(B)

The above formula has been clearly illustrated in the picture given below. 

In a similar manner, three events A, B and C are known as independent if the following conditions hold :

P (AnB)  =  P(A) x P(B)

P (BnC)  =  P(B) x P(C)

P(AnC)  =  P(A) x P(C)

P(AnBnC)  =  P(A) x P(B) x P(C)

It may be further noted that if two events A and B are independent,  then the following pairs of events are also independent:

(i)  A and B’

(ii)  A’ and B

(iii)  A’ and B’

Practice Problems

Problem 1 :

Anderson is known to hit a target in 5 out of 9 shots whereas David is known to hit the same target in 6 out of 11 shots. What is the probability that the target would be hit once they both try?

Solution :

Let A denote the event that Anderson hits the target and B, the event that David hits the target.

Probability that the target would be hit once they both try is given by 

P(AuB)  =  P(A) + P(B) - P(AnB) ------- (1)  

From the given information, we have,

P(A)  =  5/9, P(B)  =  6/11 

Here, both the events A and B are independent. 

So, we have

P(AnB)  =  P(A) x P(B)  

P(AnB)  =  (5/9) x (6/11)

P (AnB)  =  (5x6) / (9x11)

P (AnB)  =  10 / 33

Then, the required probability is

(1) -----> P(AuB)  =  P(A) + P(B) - P(AnB)

P(AuB)  =  5/9 + 6/11 - 10/33

P(AuB)  =  79 / 33

So, the required probability is 79/33.

Problem 2 :

The odds in favor of an event is 2 : 3 and the odds against another event is 3 : 7. Find the probability that only one of the two events occurs.

Solution :

We denote the two events by A and B respectively.

Then, 

P(A)  =  2 / (2+3)  =  2/5

P(B)  =  7 / (3+7)  =  7/10

As A and B are independent,

P(AnB) = P(A) x P(B)

P(AnB) = 2/5 x 7/10

P(AnB) = (2x7) / (5x10)

P(AnB) = 7/25

Probability that either only A occurs or only B occurs

=  P(A – B) + P(B – A)

=  [P(A) – P(AnB)] + [P(B) – P(AnB)]

=  P(A) + P(B) – 2 P(An B)

=  2/5 + 7/10 - 2x7/25

=  (20 + 35 - 28) / 50

=  27/50

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.