PROPERTIES OF SIMILAR TRIANGLES
Property 1 :
Two triangles are said to be similar if their corresponding sides are proportional.
Property 2 :
A perpendicular line drawn from the vertex of a right angled triangle divides the triangle into two triangles similar to each other and also to original triangle.
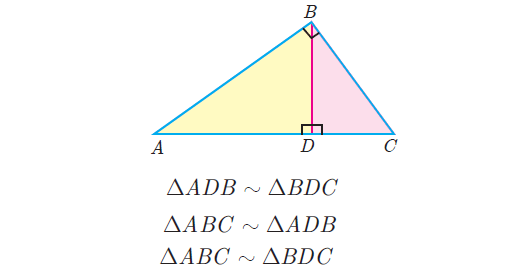
Property 3 :
If two triangles are similar, then the ratio of the corresponding sides are equal to the ratio of their corresponding altitudes.
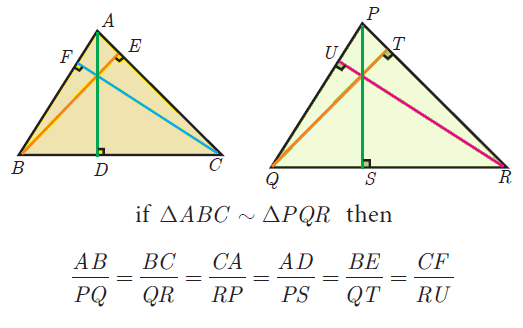
Property 4 :
If two triangles are similar, then the ratio of the corresponding sides are equal to the ratio of the corresponding perimeters.
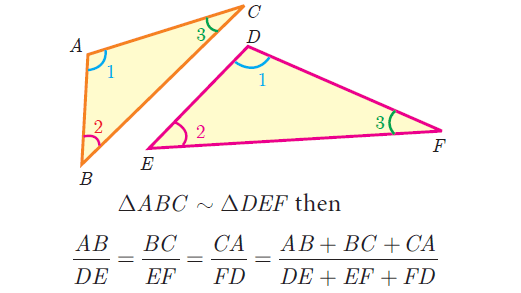
Problem 5 :
The ratio of the area of two similar triangles are equal to the ratio of the squares of their corresponding sides.
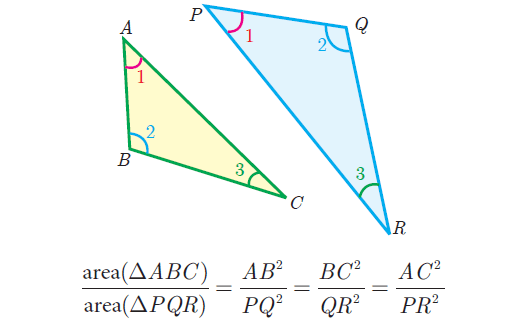
Problem 6 :
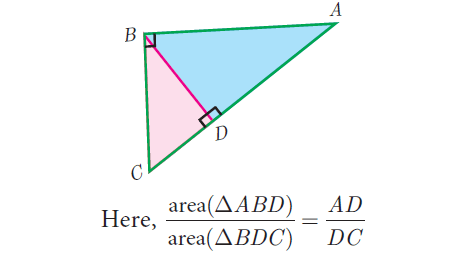
If two triangles have common vertex and their bases are on the same straight line, the ratio between their areas is equal to the ratio between the length of their bases.
Solved Problems
Problem 1 :
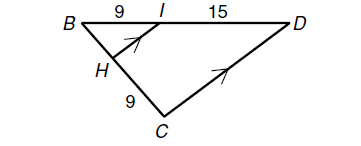
Find BH.
Solution :
The sides HI and CD are parallel.
BH/HC = BI/ID
BH/9 = 9/15
BH = 81/15
BH = 5.4
Problem 2 :
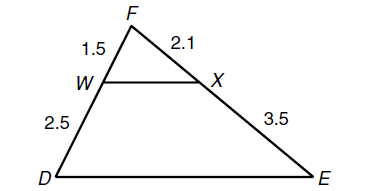
Verify WX and DE are parallel.
Solution :
Here
FW/WD = FX/XE
1.5/2.5 = 2.1/3.5
0.6 = 0.6
By Converse of Triangle Proportionality Theorem, WX and DE are parallel.
Problem 3 :
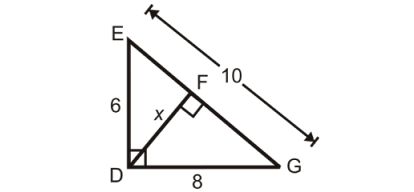
Find x.
Solution
:
EDG is a right triangle, EF is the perpendicular drawn from the right angle D.
ΔFDG, ΔEDF and ΔEDG are similar triangles to each other.
In triangles FDG and EDG.
∠DFG = ∠GDE (A)
∠FGD = ∠EGD (A)
ΔFDG ~ ΔEDG
In ΔFDG and ΔEDG :
DG/EG = DF/DE
8/10 = x/6
0.8 = x/6
Multiply both sides by 6.
4.8 = x
Problem 4 :
Find x and y.
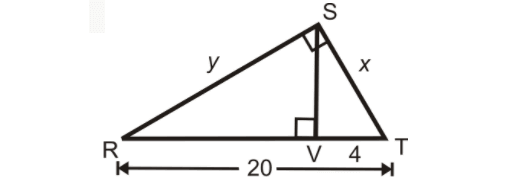
Solution :
RST is a right triangle, SV is the perpendicular drawn from the right angle S.
ΔRSV, ΔSVT and ΔRST are similar triangles to each other.
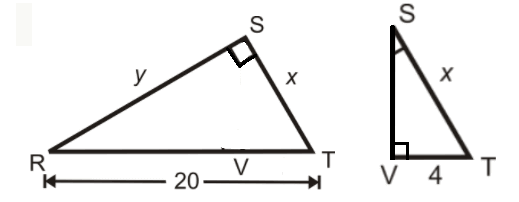
∠RST = ∠SVT (Right Angles)
∠STR = ∠STV (Reflexive Property)
By Angle-Angle Similarity Theorem,
ΔRST ~ ΔSVT
Since ΔRST ~ ΔSVT, the corresponding sides are proportional.
RT/ST = RS/SV = ST/VT
20/x = y/SV = x/4
20/x = x/4
x2 = 20(4)
x = √80
x = 4√5
In triangle RST,
RS2 + ST2 = RT2
y2 + (4√5)2 = 202
y2 + 80 = 400
Subtract 80 from both sides.
y2 = 320
Take square root on both sides.
y = √320
y = 8√5
Problem 5 :
The perimeters of two similar triangles is in the ratio 3 : 4. The sum of their areas is 75 cm2. Find the area of each triangle.
Solution :
Given : Perimeters of two similar triangles is in the ratio
3 : 4
Then,
Perimeter of the 1st Δ = 3x
Perimeter of the 2nd Δ = 4x
And also,
Area of 1st Δ : Area 2nd Δ = (3x)2 : (4x)2
Area of 1st Δ : Area 2nd Δ = 9x2 : 16x2
Given : Sum of the areas is 75 cm2.
9x2 + 16x2 = 75
25x2 = 75
Divide both sides by 25.
x2 = 3
Area of 1st Δ = 9(3) = 27 cm2
Area of 2nd Δ = 16(3) = 48 cm2
Problem 6 :
ΔHIJ ~ ΔXYZ, the ratio of their areas is 25/16, if XY has a length of 40, what is the length of HI?
Solution :
Area of ΔHIJ/Area of ΔXYZ :
= (ratio of corresponding sides)2
25/16 = (HI/XY)2
HI/XY = 5/4
Given XY = 40.
HI/40 = 5/4
HI = (5/4) ⋅ 40
HI = 50
Problem 7 :
Figure A and figure B are similar with a ratio of similarity of 5/4. If the perimeter of figure A is 18 units, what is the perimeter of figure B?
Solution :
Ratio of corresponding sides :
= Perimeter of figure A/ Perimeter of figure A
5/4 = 18/Perimeter of figure B
(Perimeter of figure B)(5/4) = 18
Perimeter of figure B = 18(4/5)
= 72/5
= 14.4
Problem 8 :
If figure A and figure B are similar and the ratio of their perimeters is 17/6, what is their ratio of similarity?
Solution :
Ratio of corresponding sides :
= Perimeter of figure A/Perimeter of figure A
Ratio of corresponding sides :
= 17/6
So, the required ratio is 17:6.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
