PROBLEMS INVOLVING INTERIOR ANGLES OF A POLYGON
Find the value of x in the following problems, give brief reasons for your answers.
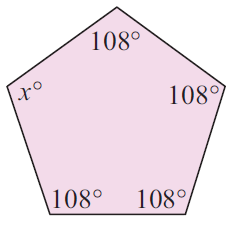
Problem 1 :
Solution
:
Number of sides of the polygon given above = 5.
Sum of interior angles of given polygon = (n - 2)180°
= (5 - 2)180°
= (3)180°
= 540°
108° + 108° + 108° + 108° + x° = 540°
432 + x = 540
Subtract 432 from both sides.
x = 108
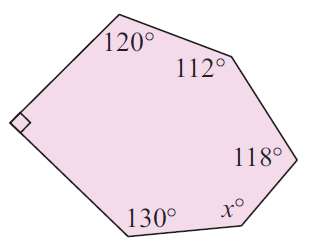
Problem 2 :
Solution
:
Number of sides of the polygon given above = 6
Sum of interior angles of given polygon = (n - 2)180°
= (6 - 2)180°
= (4)180°
= 720°
130° + x° + 118° + 112° + 120° + 90° = 720°
570 + x = 720
Subtract 570 from both sides.
x = 150
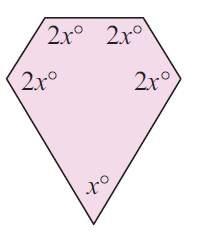
Problem 3 :
Solution
:
Number of sides = 5
Sum of interior angles of given polygon = (n - 2)180°
= (5 - 2)180°
= (3)180°
= 540°
2x° + 2x° + 2x° + 2x° + x° = 540°
9x = 540
Divide both sides by 9.
x = 60
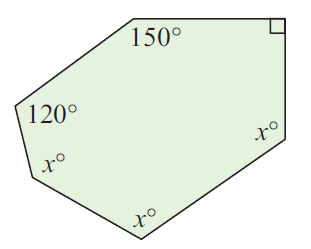
Problem 4 :
Solution
:
Number of sides = 6
Sum of interior angles of given polygon = (n - 2)180°
= (6 - 2)180°
= (4)180°
= 720°
120° + 150° + x° + x° + x° = 720°
270 + 3x = 720
Subtract 270 from both sides.
3x = 450
Divide both sides by 3.
x = 150
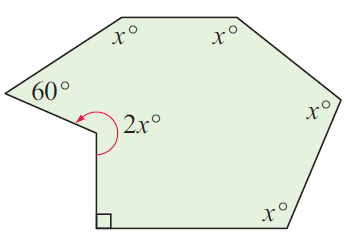
Problem 5 :
Solution
:
Number of sides = 7
Sum of interior angles of given polygon = (n - 2)180°
= (7 - 2)180°
= (5)180°
= 900°
60° + x° + x° + x° + x° + 2x° + 90° = 720°
150 + 6x = 720
Subtract 150 from both sides.
6x = 570
Divide both sides by 6.
x = 95
Problem 6 :
A regular polygon has interior angle of 156°. How many sides does the polygon have?
Solution :
Polygon is made up of a finite number of straight lines which are connected to form a closed polygonal circuit.
Sum of interior and exterior angle = 180°
Interior angle = 156°
Exterior angle = 180° - 156° = 24°
Number of sides of polygon = 360°/exterior angle
= 360°/24°
= 15
So, the polygon has 15 sides.
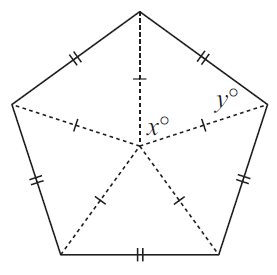
Problem 7 :
Five identical isosceles triangles are put together to form a regular pentagon.
a) Explain why 5x = 360.
b) Find x and y.
Solution
:
In each triangle, sum of interior angles = 180°
x° + y° + y° = 180°
x + 2y = 180 -----(1)
From (a)
5x = 360
Divide both sides by 5.
x = 72
Substitute x = 72 in (1).
72 + 2y = 180
Subtract 72 from both sides.
2y = 108
Divide both sides by 2.
y = 54
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Permutation Problems with Solutions
May 08, 25 12:28 PM
Permutation Problems with Solutions -
Digital SAT Math Problems and Solutions (Part - 159)
May 08, 25 01:39 AM
Digital SAT Math Problems and Solutions (Part - 159) -
Digital SAT Math Problems and Solutions (Part - 158)
May 06, 25 11:00 AM
Digital SAT Math Problems and Solutions (Part - 158)