PROBLEMS INVOLVING MAXIMUM AND MINIMUM VALUIES IN DERIVATIVES

Problem 1 :

Find the dimensions of the largest rectangle that can be inscribed in a semi circle of radius r cm.

Solution :

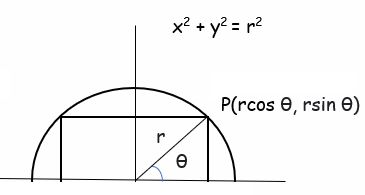
Let θ be the angle made by OP with the positive direction of x axis.

Area of rectangle A(θ)  =  (2 r cos θ) (r sinθ)

=  r² sin 2θ

A'(θ)  =  2r² cos 2θ

A'(θ)  =  0

2r² cos 2θ  =  0

2θ  =  cos^-1(0)

2θ  =  π/2

θ  =  π/4

A''(θ)  =  -4r² sin 2θ

A''(π/4)  =  -4r² sin 2(π/4)

A''(π/4)  =  -4 r² < 0 (Maximum)

Length of the rectangle  =  2r cos θ  =  2rcos(π/4)

=  2 r (1/√2)

=  2 r (1/√2)

=  √2r

Width of the rectangle  =  r sin θ

=  r sin (π/4)

=  r (1/√2)

=  r/√2

Problem 2 :

A manufacturer wants to design an open box having a square base and a surface area of 108 sq.cm. Determine the dimensions of the box for the maximum volume.

Solution :

Let x be the side length of square base box.

Volume of the box  =  length x width x height

Let h be the height 

Surface area of box  =  x² + 4xh

x² + 4xh  =  108

4xh  =  108-x²

h  =  (108-x²)/4x  ---(1)

Volume of the box  =  Base area x height

V(x)  =  x² (h)  ---(2)

V(x)  =  x²(108-x²)/4x

V(x)  =  (108x-x³)/4

V'(x)  =  (108 - 3x²)/4

V'(x)  =  0

(108 - 3x²)/4  =  0

3x²  =  108

x²  =  36

x  =  6

V''(x)  =  -6x/4

V''(x)  =  -3x/2

V''(6)  =  -3(6)/2

V''(6)  =  -9 < 0 (Maximum)

Applying x  =  6 in (1), we get

h  =  (108-x²)/4x

h  =  (108-36)/24

h  = 3 cm

So, side length of the base is 4 cm and height is 3 cm.

Problem 3 :

The volume of a cylinder is given by the formula

V  =  π r²h

Find the greatest and least values of V if r + h = 6.

Solution :

Given :

V  =  π r²h and r + h  =  6

h  =  6 - r

V(r)  =  π r²(6-r)

V(r)  =  π(6r²-r³)

V'(r)  =  π(12r-3r²)

V'(r)  =  0

3rπ(4-r)  =  0

r  =  0 and r  =  4

r+h  =  6

Case 1 : When r  =  0, h  =  6

Case 2 : When r  =  4, h  =  2

V  =  π r²h

By applying case 1,  V  =  0

By applying case 2,  V  =  π (4)²(2)  ==>  32π

So, the greatest value of V is 32π and least value of V is 0.

Problem 4 :

A hollow cone with base radius a cm and height b cm is placed on a table. Show that the volume of the largest cylinder that can be hidden underneath is 4/9 times volume of the cone.

Solution :

Volume of cone  =  (1/3)π r²h----(1)

Here r  =  a and h  =  b

=  (1/3)π r²h

=  (1/3)π a²b

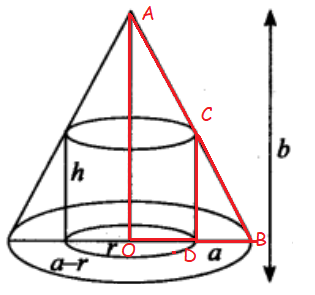
OAB and CDB are similar.

OA/DC  =  OB/DB

b/h  =  a/(a-r)

h  =  (b/a)(a-r)

V(r)  =  (1/3)π r²[(b/a)(a-r)]

V(r)  =  (b/3a)π r²(a-r)

V(r)  =  (bπ/3a) (ar²-r³)

V'(r)  =  (bπ/3a) (2ar-3r²)

V'(r)  =  (bπ/3a) (2ar-3r²)  =  0

r(2a-3r)  =  0

r  =  0, r  =  2a/3

V''(r)  =  (bπ/3a) (2a-6r)

V''(0)  =  (bπ/3a) (2a) > 0 Minimum

V''(r)  =  (bπ/3a) (2a-6(2a/3))

V''(2a/3)  =  (bπ/3a) (2a-6(2a/3)) < 0 Maximum

Volume of cylinder  =  πr²h

r  =  2a/3 and h  =  (b/a)(a-(2a/3))

h  =  (b/a) (a/3)

h  =  b/3

=  π(2a/3)²(b/3)

Volume of cylinder  =  (4/9)(1/3)πa²b

Volume of cylinder  =  (4/9)Volume of cone

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.