PROBLEMS INVOLVING VERTICALLY OPPOSITE ANGLES
What is vertically opposite angles ?
The pair of angles that are opposite each other measure the same number of degrees and are equal.
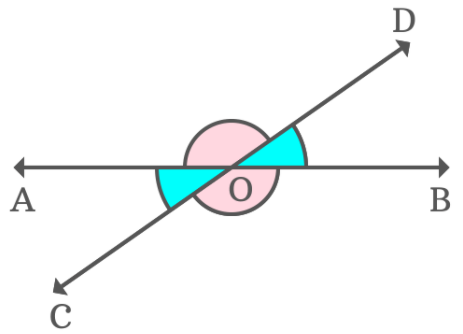
<COD + <AOD = 180 -------(1)
<COB + <BOD = 180 -------(2)
(1) = (2)
<COD + <AOD = <COB + <BOD
Find the value(s) of the variable(s) :
Example 1 :
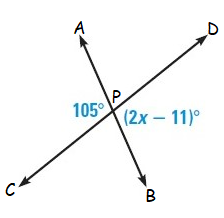
Solution :
In the given figure,
<APC = <BPD (vertically opposite angles)
Here <APC = 105˚ and <BPD = (2x – 11)˚
105˚ = (2x – 11)˚
105˚ + 11˚ = 2x˚
116˚ = 2x
x = 58˚
So, the value of x is 58˚
Example 2 :
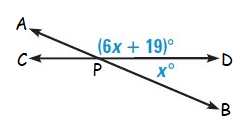
Solution :
In the given figure,
<APD = (6x + 19)˚ (vertical angle)
<BPD = x˚ (adjacent angle)
We know that a vertical angle and its adjacent angle are supplementary angles.
So,
<APD + <BPD = 180˚
(6x + 19)˚ + x˚ = 180˚
6x˚ + 19˚ + x˚ = 180˚
7x˚ = 180˚ - 19˚
7x˚ = 161˚
x = 23˚
So, the value of x is 23˚
Example 3 :
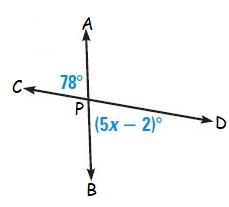
Solution :
In the given figure,
<APC = <BPD (vertically opposite angles)
Here <APC = 78˚ and <BPD = (5x – 2)˚
78˚ = (5x – 2)˚
78˚ + 2˚ = 5x˚
80˚ = 5x
x = 16˚
So, the value of x is 16˚
Example 4 :
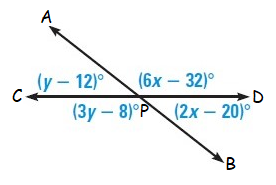
Solution :
In the given figure,
<APD = (6x - 32)˚ (vertical angle)
<BPD = (2x – 20)˚ (adjacent angle)
We know that a vertical angle and its adjacent angle are supplementary angles.
So,
<APD + <BPD = 180˚
6x - 32˚+ 2x - 20˚ = 180˚
8x – 52˚ = 180˚
8x
= 232˚
x = 29˚
Then,
<APC = (y – 12)˚ (vertical angle)
<BPC = (3y – 8)˚ (adjacent angle)
So,
<APC + <BPC = 180˚
y – 12˚ + 3y – 8˚ = 180˚
4y - 20˚ = 180˚
4y = 180˚ + 20˚
4y = 200˚
y = 50˚
Example 5 :
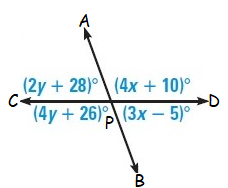
Solution :
In the given figure,
<APD = (4x + 10)˚ (vertical angle)
<BPD = (3x – 5)˚ (adjacent angle)
So,
<APD + <BPD = 180˚
4x + 10˚+ 3x - 5˚ = 180˚
7x + 5˚ = 180˚
7x = 180˚ - 5˚
7x = 175˚
x = 25˚
Then,
<APC = (2y + 28)˚ (vertical angle)
<BPC = (4y + 26)˚ (adjacent angle)
<APC + <BPC = 180˚
2y + 28˚ + 4y + 26˚ = 180˚
6y + 54˚ = 180˚
6y = 180˚ - 54˚
6y = 126˚
y = 21˚
Example 6 :
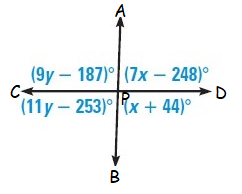
Solution :
In the given figure,
<APD = (7x - 248)˚ (vertical angle)
<BPD = (x + 44)˚ (adjacent angle)
So,
<APD + <BPD = 180˚
7x - 248˚+ x + 44˚ = 180˚
8x - 204˚ = 180˚
8x = 180˚ + 204˚
8x = 384˚
x = 48˚
Then,
<APC = (9y - 187)˚ (vertical angle)
<BPC = (11y - 253)˚ (adjacent angle)
So,
<APC + <BPC = 180˚
9y - 187˚ + 11y - 253˚ = 180˚
20y - 440˚ = 180˚
20y = 180˚ + 440˚
20y = 620˚
y = 31˚
Example 7 :
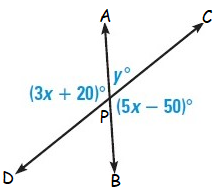
Solution :
In the given figure,
<APD = <BPC (vertically opposite angles)
Here <APD = (3x + 20)˚ and <BPD = (5x – 50)˚
3x + 20˚ = 5x – 50˚
3x - 5x = -50˚ - 20˚
-2x = -70˚
x = 35˚
Then,
<APC = y˚ (vertical angle)
<BPC = (5x - 50)˚ (adjacent angle)
So,
<APC + <BPC = 180˚
y˚ + 5x - 50˚ = 180˚
y˚ + 5(35˚) - 50˚ = 180˚
y + 175˚ - 50˚ = 180˚
y + 125˚ = 180˚
y = 180˚ - 125˚
y = 55˚
Example 8 :
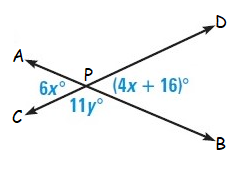
Solution :
In the given figure,
<APC = <BPD (vertically opposite angles)
Here <APC = 6x˚ and <BPD = (4x + 16)˚
6x˚ = 4x + 16˚
6x - 4x = 16˚
2x = 16˚
x = 8˚
Then,
<APC = 6x˚ (vertical angle)
<BPC = 11y˚ (adjacent angle)
So,
<APC + <BPC = 180˚
6x˚ + 11y˚ = 180˚
6(8˚) + 11y˚ = 180˚
48˚ + 11y˚ = 180˚
11y˚ = 180˚ - 48˚
11y = 132˚
y = 12˚
Example 9 :
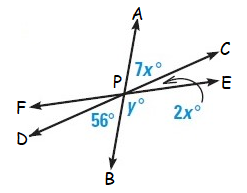
Solution :
In the given figure,
<APC = <BPD (vertically opposite angles)
Here <APC = 7x˚ and <BPD = 56˚
7x˚ = 56˚
x = 8˚
Then,
<CPE = 2x˚ (vertical angle)
<BPE = y˚ (adjacent angle)
So,
<APC + <BPC = 180˚
2x˚ + y˚ = 180˚
2(8˚) + y˚ = 180˚
16˚ + y˚ = 180˚
y˚ = 180˚ - 16˚
y = 164˚
Example 10 :
l and m are parallel and a line t intersects these lines at P and Q, respectively. Find the sum 2a + b.
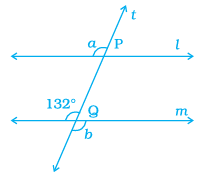
Solution :
- 132 and b are vertically opposite angles.
- 132 and a are corresponding angles.
Example 11 :
In the accompanying diagram, parallel lines 𝐻𝐸 and 𝐴𝐷 are intersected by transversal 𝐵𝐹 at G and C, respectively.
If 𝑚 < 𝐻𝐺𝐹 = 5𝑛 and 𝑚 < 𝐵𝐶𝐷 = 2𝑛 + 66, what is 𝑚 < 𝐻𝐺𝐹 and 𝑚 < 𝐹𝐺𝐸?
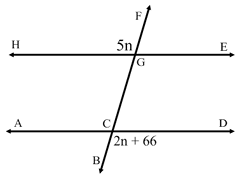
Solution :
<HGF = <ACG (vertically opposite angles)
5n = 2n + 66
5n - 2n = 66
3n = 66
n = 66/3
n = 22
𝑚 < 𝐻𝐺𝐹 = 5(22)
= 110
𝑚 < 𝐹𝐺𝐸 = 180 - 110
= 70
Example 12 :
Given: 𝑚 < 3 = 3𝑥 + 30 and 𝑚 < 7 = 5𝑥
a) The relationship is:
b) The equation is:
c) Angle 3
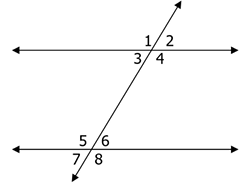
Solution :
𝑚 < 3 = 3𝑥 + 30 and 𝑚 < 7 = 5𝑥
These angles are corresponding angles.
3x + 30 = 5x
30 = 5x - 3x
30 = 2x
x = 30/2
x = 15
To find angle measure 3, we apply the value of x in 3x + 30
= 3(15) + 30
= 45 + 30
= 75
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 146)
Apr 18, 25 06:52 AM
Digital SAT Math Problems and Solutions (Part - 146) -
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145)

