PROBLEMS ON CIRCLES IN CONIC SECTIONS

Problem 1 :

The equation of the circle passing through (1, 5) and (4, 1) and touching y-axis is

x² + y² - 5x - 6y + 9 +λ(4x+3y-19) = 0

where λ is equal to 

a)  0, -40/9   b)  0    3)  40/9    d)  -40/9

Solution :

x² + y² - 5x - 6y + 9 +λ(4x+3y-19) = 0

x²+ y² - 5x + 4λx - 6y + 3λy+ 9 -19λ = 0

x²+ y² + (4λ - 5)x + (3λ - 6)y + 9 -19λ = 0

The circle touches y-axis, then x = 0

y² + (3λ - 6)y + 9 -19λ = 0

Since the circle touches y-axis, it will have equal real roots.

b² - 4ac = 0

(3λ - 6)² - 4(1)(9 -19λ) = 0

Option a :

λ = 0 and λ = -40/9

these are the values satisfying the equation. So, option a is correct.

Problem 2 :

The circle x² + y² = 4x + 8y + 5 intersects the line 3x - 4y = m at two distinct points if 

a)  15 < m < 65   b)  35 < m < 85

3)  -85 < m < -35    d)  -35 < m < 15

Solution :

x² + y² = 4x + 8y + 5

x² + y² - 4x - 8y - 5 = 0

Comparing the equation with x² + y² + 2gx + 2fy + c = 0

2g = -4, 2f = -8

g = -2, f = -4, c = -5

Center of the circle will be (-g, -f) ==> (2, 4)

radius = √g²+f²-c

= √2²+4²-(-5)

= √4+16+5

= 5

Length of perpendicular from the point (2, 4) will be lesser than the radius.

So, option d is correct.

Problem 3 :

The length of the diameter of the circle which touches the x-axis at the point (1, 0) and passes through the point (2, 3).

Solution :

Let (h, k) be the center of the circle and r be the radius.

(x - h)² + (y - k)² = r

The circle is passing through the point (1, 0).

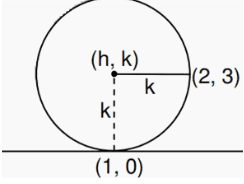
The vertical distance between (1, 0) to the center is k. Then the distance between (h, k) and (2, 3) will be the same because they are radii.

(1 - h)² + (0 - k)² = k²

(1 - h)² = 0

1 - h = 0

h = 1

The circle passes through the point (2, 3). 

(2 - h)² + (3 - k)² = r

Applying the value of h

(2 - 1)² + (3 - k)² = k²

1 + 9 - 6k + k² = k²

-6k = -10

k = 10/6

k = 5/3

Problem 4 :

The radius of the circle 3x² + by² + 4bx - 6by + b² = 0

a)  1       b)  3      c)  √10       d)  √11

Solution :

3x² + by² + 4bx - 6by + b² = 0

If the given equation represents equation of circle then, it will have the following characteristics.

i) it is a second degree equation in x and y.

ii) Coefficient of x² = coefficient of y² 

iii)  Coefficient of xy = 0

Using the second property, b = 3.

3x² + 3y² + 12x - 18y + 9 = 0

Dividing by 3, we get

x² + y² + 4x - 6y + 3 = 0

2g = 4 ==> g = 2

2f = -6 ==> f = -3

and c = 3

Finally g = 2, f = -3 and c = 3

radius = √g² + f² - c

= √2² + (-3)² - 3

= √4 + 9 - 3

= √10

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.