PROBLEMS ON EVALUATING DEFINITE INTEGRALS

Evaluate the following definite integrals :

Problem 1 :

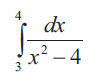
Solution :

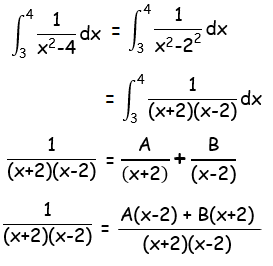
1 = A(x-2) + B(x+2)

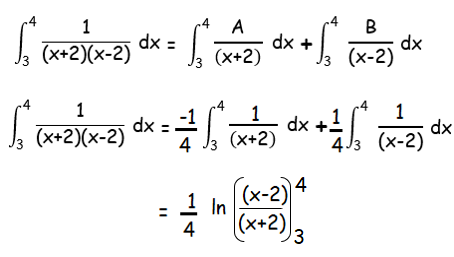
By applying the limits, we get

= (1/4) [ln(2/6) - ln(1/5)]

= (1/4) [ln (2/6) ⋅ (5/1)]

= (1/4) [ln (5/3)]

Problem 2 :

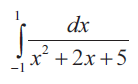
Solution :

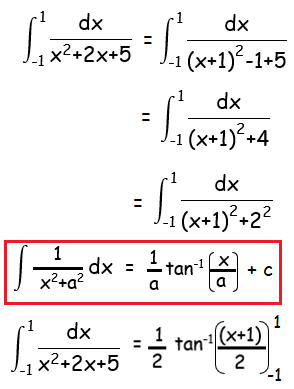
By applying the limits, we get

= (1/2) [tan^-1(2/2) - tan^-1(0)]

= (1/2) [π/4 - 0]

= π/8

Problem 3 :

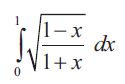
Solution :

Let us apply trigonometric substitution.

x = cos2θ

(1-x)/(1+x) = (1-cos2θ)/(1+cos2θ)

= sin²θ/cos²θ

= tan²θ

dx = -2sin 2θ dθ

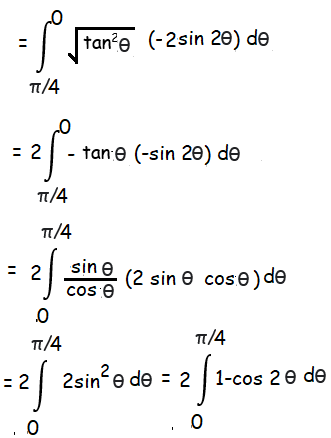
By integrating

= 2[θ-sin2θ/2]

= 2(π/4 - sin2(π/4)/2)

= π/2 - 1

Problem 4 :

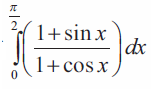
Solution :

1+sinx :

sin 2x = 2tanx/(1+tan²x)

Dividing x by 2 on both sides, we get

sin x = 2tan(x/2)/(1+tan²(x/2))

1 + sinx = [1+tan²(x/2) + 2tan(x/2)] / (1+tan²(x/2))

1 + sinx = [1+tan²(x/2) + 2tan(x/2)] / (1+tan²(x/2))  ---(1)

cos 2x = (1-tan²x)/(1+tan²x)

Dividing x by 2 on both sides, we get

cos x = (1-tan²(x/2)/(1+tan²(x/2))

1 + cosx = 1 + [(1-tan²(x/2)/(1+tan²(x/2))]

= [(1+tan²(x/2) + (1-tan²(x/2)] / (1+tan²(x/2))

1 + cosx = 2/(1+tan²(x/2)) ----(2)

(1) / (2)

(1+sinx)/(1+cosx) = [1+tan²(x/2) + 2tan(x/2)]/2

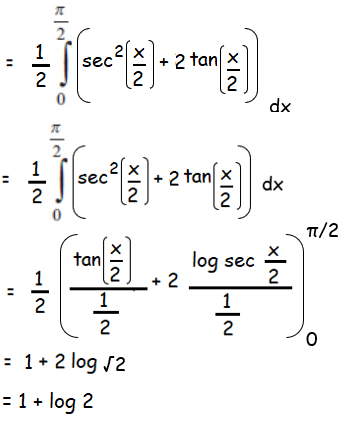
Problem 5 :

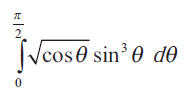
Solution :

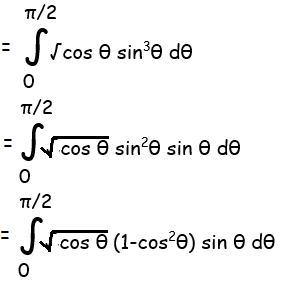
Let t = cos θ

dt = -sin θ dθ ==>  sin θ dθ = -dt

When θ = 0, t = cos 0 ==> 1

When θ = π/2, t = cos π/2 ==> 0

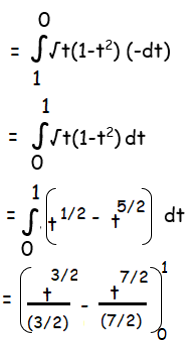
By applying the limit, we get

= (2/3) (1)^3/2 - (2/7) (1)^7/2 - 0

= (2/3) - (2/7)

= (14-6)/21

= 8/21

Problem 6 :

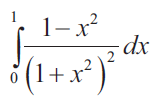
Solution :

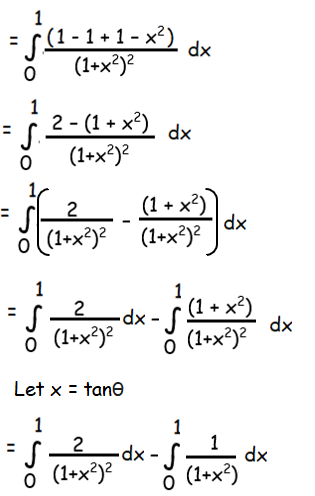
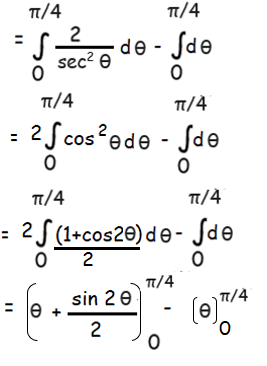
By applying the limits, we get

= [sin 2(π/4)]/2

= 1/2

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.