PROBLEMS ON INTERNAL AND EXTERNAL TANGENTS OF A CIRCLE

Problem 1 :

A circle with a radius of 8 cm is externally tangent to a circle with a radius of 18 cm. Find the length of the external tangent.

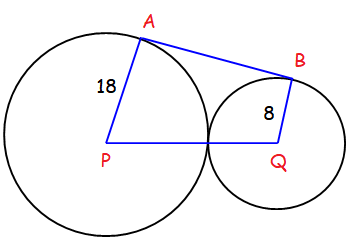
Solution :

When we join the point from Q on the side AP, we get a rectangle ABCQ and triangle CPQ.

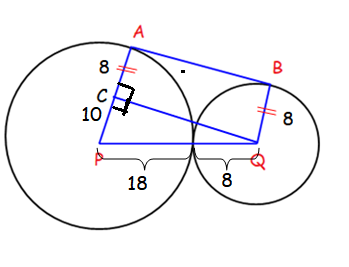
In triangle CPQ :

PQ  =  18+8  ==>   26

PQ²  =  CP² + CQ² 

26²  =  10² + CQ² 

676 - 100  =  CQ² 

CQ²  =  576

CQ  =  √576

CQ  =  24

CQ  =  AB  =  24 cm

So, length of external tangent is 24 cm.

Problem 2 :

The center of two circles of radii 10 cm and 5 cm are 13 cm apart.

(a)  Find the length of external tangent.

(b)  Do the circles intersect.

Solution :

Let us draw a rough picture.

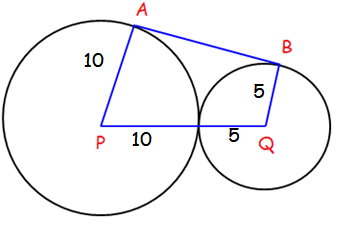
The picture drawn above does not satisfy the condition.  Because in the picture given above, the length of PQ is 15 but according to the given information the length between their centers is 13.

So, we draw the picture 

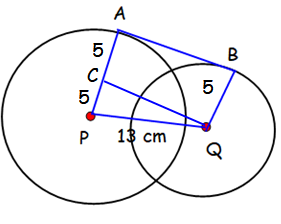
In triangle CPQ :

PQ  =  13 (given)

PQ²  =  CP² + CQ² 

13²  =  5² + CQ² 

169 - 25  =  CQ² 

CQ²  =  144

CQ  =  √144

CQ  =  12

CQ  =  AB  = 12 cm

So, length of external tangent is 12 cm.

(b) Yes, both circles are touching at 2 points.

Problem 3 :

RD is a tangent to a circle A and H. HA  =  40 cm, the radius of circle A is 8 cm and radius of circle H is 12 cm. Find the length of RD.

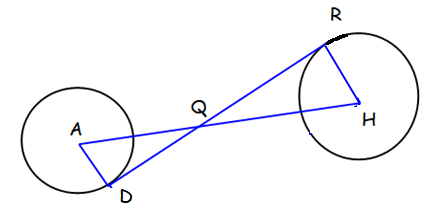
Solution :

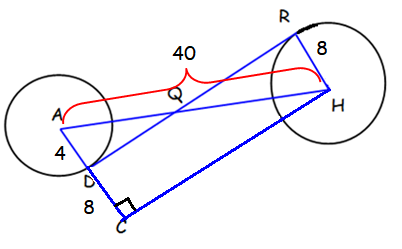
When we draw a line from D and that is parallel to RH, it becomes the shape rectangle RHDC.

Triangle AHC is a right triangle.

<ACH  =  90 degree

AC  =  AD + DC ==>  12, RH  =  8and AH  =  40

Using Pythagorean theorem, we get 

AH²  =  AC² + CH² 

40²  =  12² + CH² 

1600 - 144  =  CH² 

CH²  =  1456

CH  = √1456

CH  =  38.15

RD  =  38.15

So, the length of external tangent is 38.15 cm. 

Problem 4 :

AB is tangent to both circles. Find the value of x and the distance between the centers.

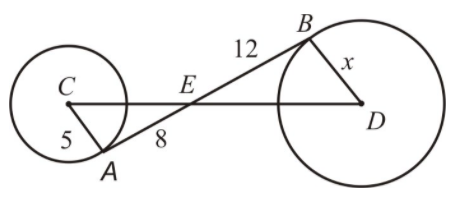
Solution :

Triangle CEA is right triangle.

CE²  =  AC² + AE²

CE²  =  5² + 8²

CE²  =  89

CE  =  √89

In triangle CEA and triangle EBD

<CAE  =  <BDE (A)

<CEA  =  <BED (A)

Using AA, triangles CEA and EBD are similar.

So, their corresponding sides will be the same ratio.

CE/ED  =  CA/BD  =  AE/EB

√89/ED  =  5/x  =  8/12

5/x  =  8/12

x  =  60/8

x  =  7.5

√89/ED  =  5/x

By applying the value of x above, we get

√89/ED  =  5/7.5

9.4(7.5)/5  =  ED

ED  =  14.1

Distance between centers  =  CD

  =  CE + ED

  =  9.4+14.1

  =  23.5

So, distance between two centers is 23.5 cm.

Problem 5 :

Two circles that are externally tangent have radii 12 inches and 8 inches respectively. Find the length of the tangent AB.

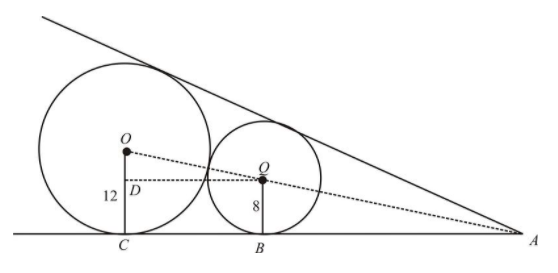
Solution :

DC  =  8 inches and let OD  =  x.

In triangles AQB and AOC,

<QAB  =  <OAC

<ABQ  =  <ACO (90)

Using AA, 

ΔAQB ~ ΔAOC

Corresponding sides will be in the same ratio.

OB/OC  =  AQ/AO  =  AB/AC

8/12  =  AQ/(20+AQ)  =  AB/AC

2/3  =  AQ/(20+AQ)

2(20+AQ)  =  3AQ

AQ  =  40

In triangle AQB, using Pythagorean theorem

QA²  =  OB² + AB²

40²  =  8² + AB²

1600-64  =  AB²

AB  =  √1536

AB  =  39.2

So, length of tangent AB is 39.2 cm.

Problem 6 :

For the circle with center P the tangent of each side of ABCD, AB = 20, BC = 15 and CD = 12, find AD.

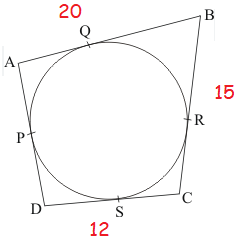
Solution :

Since the length of tangents drawn from the external points will be equal, we consider BQ = x, then BR = x

AQ = 20 - x, RC = 15 - x, DS = 12 - (15 - x)

DS = 12 - 15 + x ==> -3 + x

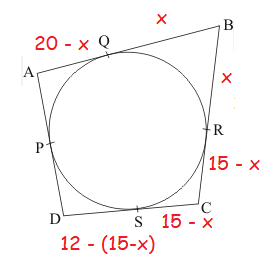
PD = -3 + x and AP = 20 - x

AP + PD = AD

20 - x + (-3 + x) = AD

AD = 20 - x - 3 + x

AD = 17

So, the length of AD is 17.

Problem 7 :

Given that circles A, B and C are tangents and that AB = 8, BC = 13 and AC = 11, find the radii of all three circles.

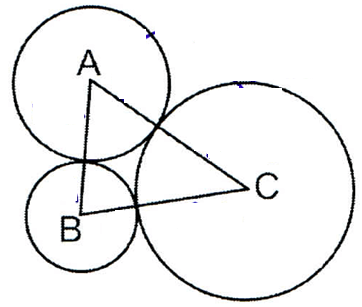
Solution :

AB = 8

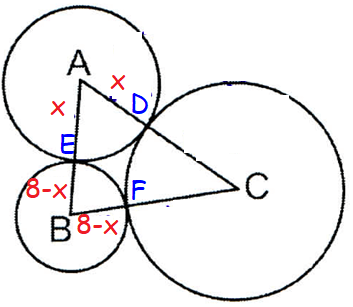
Let AE = x, then BE = 8 - x, BF = 8 - x

BC = 13, CF = 13 - (8 - x)

= 13 - 8 + x

CF = 5 + x and DC = 5 + x

AC = 11

AD + DC = 11

x + 5 + x = 11

2x + 5 = 11

2x = 11 - 5

2x = 6

x = 3

AD = 3 (radius of circle A)

BE = 8 - 3

BE = 5 (radius of circle B)

CF = 5 + x

= 5 + 3

CF = 8 (radius of circle C)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.