PROBLEMS ON INTERNALLY AND EXTERNALLY TANGENT CIRCLES

Problem 1 :

In the picture given below. CD is tangent of both circles.

AB  =  20, AC  =  15 and BD  =  10. Find CD.

Solution :

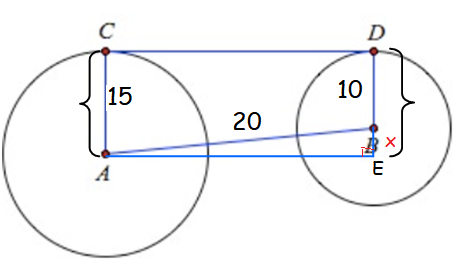
In triangle ABE,

AC  =  DE  =  15

So, x  =  BE  =  5

<AEB  =  90

Using Pythagorean theorem,

AB²  =  AE²+BE²

20²  =  AE²+5²

400-25  =  AE²

AE  =  √375

AE  =  19.3

AE  =  CD  =  19.3

So, length of common tangent is 19.3 cm.

Problem 2 :

AB  =  24, AC  =  18 and CD  =  19. Find BD.

Solution :

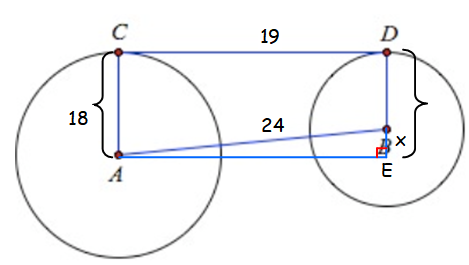
Let BE  =  x.

In triangle ABE,

<AEB  =  90 degree

AB²  =  AE²+EB²

24²  =  19²+x²

576 - 361  =  x²

x  =   √215

x  =  14.66

BD  =  DE-BE

BD  =  18-14.66

BD  =  3.34

So, BD is 3.34.

Problem 3 :

AC is tangent to both circles. Find the measure of angle ∠CQB

If AO=9 and AB=15

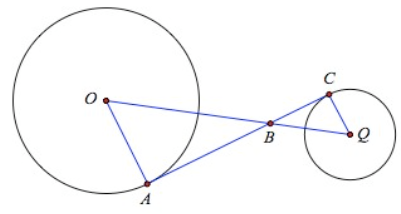
Solution :

In triangles OAB, BCQ

<OAB  =   <BCQ  (90 degree)

<OBA  =  <CBQ  (Vertically opposite angles)

So,

<AOB  =  <CQB

In triangle OAB,

OA  =  9 and AB  =  15

OB²  =  OA² + AB²

OB²  =  9² + 15²

OB  =  √(81+225)

OB  =  √306

OB  =  17.49

cos θ  =  Adjacent / Hypotenuse

cos <AOB  =  OA/OB

cos <AOB  =  9/17.49

cos <AOB  =  0.514

<AOB  =  cos^-1(0.514)

<AOB  =  59.06

<AOB  =  59  =  <CQB

So, the required angle is 59.

Problem 4 :

Find x, if DC  =  2x+3 and EC  =  x+10

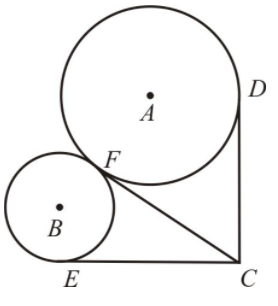
Solution :

Length of tangents drawn from out of the circle will be equal.

So,

DC  =  EC

2x+3  =  x+10

x  =  7

Problem 5 :

Four identical coins are lined up in a row as shown. The distance between the centers of the first and the fourth coin is 42inches. What is the radius of one of the coins? 

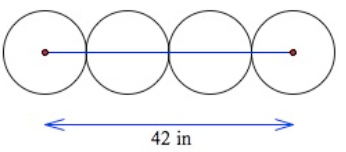
Solution :

Let "r" be the radius of one circle.

r+2r+2r+r  =  42

6r  =  42

r  =  42/6

r  =  7

So, radius of one circle is 7 cm.

Problem 6 :

Four circles are arranged inside an equilateral triangle as shown. If the triangle has sides equal to 16cm , what is the radius of the bigger

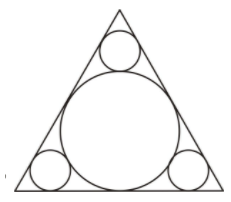
Solution :

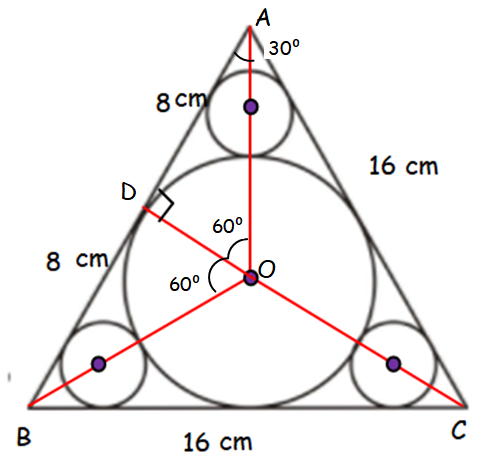
In triangle ADC

tanθ  =  Opposite side/Adjacent side

tan 60  =  DA/DO

√3  =  8/DO

DO  =  8/√3

DO  =  4.618

Approximately 4.62.

So radius if the larger circle is 4.62 cm.

Problem 7 :

In diagram, circle O is inscribed in triangle ABC. If AB = 6, AF = 4 and EC = 3, what is the perimeter of triangle ABC ?

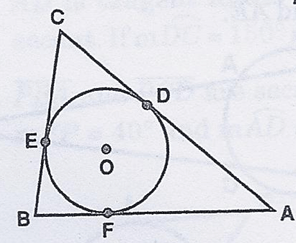
Solution :

Lengths of tangents drawn from the external point will be equal.

AB = 6, AF = 4

When AF = 4, then AD = 4

AB = AF + BF

6 = 4 + BF

BF = 6 - 4

BF = 2 then BE = 2

CE = 3 then DC = 3

Perimeter of the triangle ABC = AB + BC + CA

= (AF + BF) + (BE + EC) + (CD + DA)

= (4 + 2) + (2 + 3) + (3 + 4)

= 6 + 5 + 7

= 18

So, perimeter of the triangle is 18 units.

Problem 8 :

In the diagram,  circle O is inscribed in quadrilateral ABCD and E, F, G and H are the points of tangency of the sides. If AH = 6, DG = 4 and CF = 2 and BF = 3, what is the perimeter of the quadrilateral ABCD ?

a)  15    b)  21     c)  24      d)  30

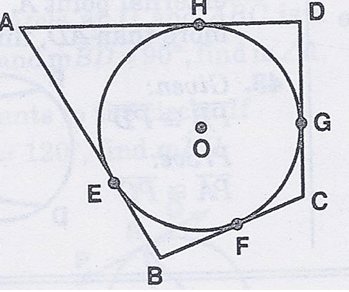
Solution :

Length of tangents drawn from the point away from the circle.

Given that,

AH = 6, then AE = 6

DG = 4, then DH = 4

CF = 2, then CG = 2

BF = 3, then BE = 3

Perimeter of quadrilateral ABCD :

= AB + BC + CD + DA

= (AE + BE) + (BF + FC) + (CG + DG) + (DH + AH)

= (6 + 3) + (3 + 2) + (2 + 4) + (4 + 6)

= 9 + 5 + 6 + 10

= 30

So, the perimeter of quadrilateral ABCD is 30 units. Option d is correct.

Problem 9 :

In the diagram, PAB and PCD are externally tangent to circle O and O'. IF PB = 16 and CD = 10, find PA.

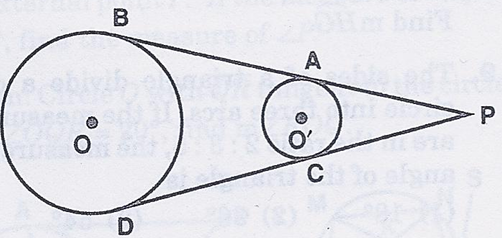
Solution :

PB = 16

PB is the tangent drawn from the point away from the circle.

PA is the tangent drawn from the point away from circle to the circle with center O'. Similarly PC is also the tangent drawn from the same point to the same circle. 

Then, lengths of PA and PC will be equal.

PB is the tangent drawn from the point away from circle to the circle with center O. Similarly PD is also the tangent drawn from the same point to the same circle.

Then, lengths of PB and PD will be equal.

PB = 16 -----(1)

PA + AB = 16

PD = PC + CD

PD = PC + 10 -----(2)

(1) = (2)

16 = PC + 10

PC = 16 - 10

PC = 6

PC = PA = 6

So, the length of tangent PA is 6.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.