PROBLEMS ON PROPERTIES OF RHOMBUS

Problem 1 :

Three vertices of a rhombus taken in order are 

(2, −1), (3, 4) and (−2, 3) 

find the fourth vertex.

Solution :

Let the given points be A (2, −1), B (3, 4) and C (−2, 3) and the required point be D (a, b).

Midpoint of diagonal AC  =  Midpoint of diagonal BD

Midpoint of diagonal AC  =  (x₁ + x₂)/2, (y₁ + y₂)/2

Midpoint of diagonal AC  =  (2 - 2)/2, (-1 + 3)/2

  =  (0, 1) ----(1)

Midpoint of diagonal BD  =  (3 + a)/2, (4 + b)/2 ----(2)

(1)  =  (2)

(3 + a)/2, (4 + b)/2  =  (0, 1)

So, the required vertex is (-3, -2).

Problem 2 :

Assume quadrilateral EFGH is a rhombus. If the perimeter of EFGH is 24 and the length of diagonal EG = 10, what is the length of diagonal FH?

Solution :

Perimeter of rhombus  =  24

4a  =  24

a  =  6

Side length of rhombus is 6 

Length of diagonal  =  10

In rhombus, we have four right triangles.

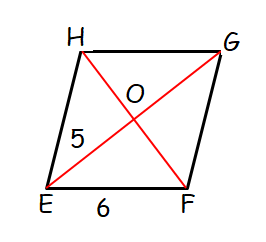
In triangle OEF

OE  =  5

Half length of diagonal FH  =  x

10²  =  5² + x²

100 - 25  =  x²

x²  =  75

x  =  5√3

Problem 3 :

If the area of a rhombus is 112 cm² and one of its diagonal is 14 cm find its other.

Solution :

Area of rhombus  =  (d₁ ⋅ d₂)/2

d₁  =  14 cm, d₂  =  ?

Area  =  112 cm²

 (14 ⋅ d₂)/2  =  112

d₂  =  112(2)/14

d₂  =  16

So, the other diagonal is 16 cm.

Problem 4 :

The length of diagonal are ratio 5:4 area of rhombus is 2250 cm² find the length of diagonals.

Solution :

Length of diagonals are 5x and 4x.

Area of rhombus  =  2250 cm²

 (5x ⋅ 4x)/2  =  2250

20x²  =  4500

x²  =  225

x  =  15 cm

5x  =  5(15)  ==>  75

4x  =  4(15)  ==>  60

Length of diagonals are 75 cm and 60 cm.

Problem 5 :

If opposite angles of a rhombus are (2x)° and (3x-40)° then value of x is ?

Solution :

In a rhombus, opposite angles will be equal. 

2x  =  3x-40

x  =  40

Problem 6 :

ABCD is a rhombus in which AB is 3x-2, AC is 4x+4 and BD is 2x. Find x.

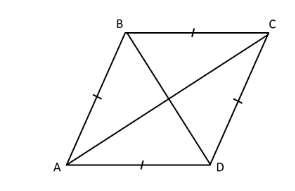
Solution :

AB  =  AD  =  3x-2

AC/2  =  (4x + 4)/2 ==>  2x + 2

BD/2  =  2x/2 ==>  2

(3x - 2)²  =  (2x + 2)² + x²

9x² + 4 - 12x  =  4x² + 8x + 4 + x²

4x² - 12x - 8x + 4 - 4  =  0

4x² - 20x  =  0

4x(x - 5)  =  0

x can not be 0.

So, x  =  5.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.