PROBLEMS ON QUADRATIC EQUATIONS
Problem 1 :
Find the value of
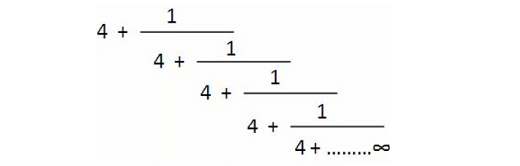
Solution :
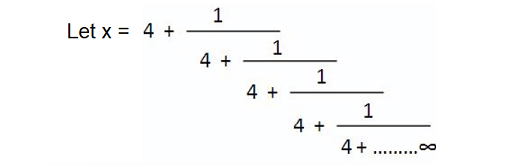
Then,
The quadratic equation above can not be solved by factoring. So, we can use quadratic formula and solve.
Comparing ax2 + bx + c = 0 and x2 - 4x - 1 = 0,
a = 1, b = -4 and c = -1
Quadratic formula :
Substitute a = 1, b = -4 and c = -1.
When we look at the given numerical expression, it is clear that its value must be greater than 4.
Therefore the value of the given numerical expression is
2 + √5
Problem 2 :
Solve for x in the following equation :
4x - 3 ⋅ 2x+2 + 25 = 0
Solution :
4x - 3 ⋅ 2x+2 + 25 = 0
(2x)2 - 3 ⋅ 2x ⋅ 22 + 32 = 0
(2x)2 - 3 ⋅ 2x ⋅ 4 + 32 = 0
(2x)2 - 12 ⋅ 2x + 32 = 0
Let y = 2x.
y2 - 12y + 32 = 0
(y - 8)(y - 4) = 0
y - 8 = 0 or y - 4 = 0
y = 8 or y = 4
Replace y by 2x.
2x = 8 or 2x = 4
2x = 23 or 2x = 22
x = 3 or x = 2
So, the values of x are 3 and 2.
Problem 3 :
If the sum of the roots of the quadratic equation
ax2 + bx + c = 0
is equal to the sum of the squares of their reciprocals, then find the value of
(b2/ac) + (bc/a2)
Solution :
Let 'α' and 'β' be the roots of the equation
ax2 + bx + c = 0
Given : Sum of the roots is equal to the sum of the squares of their reciprocals .
α + β = (1/α)2 + (1/β)2
α + β = 1/α2 + 1/β2
α + β = (α2 + β2)/(α2β2)
α + β = [(α + β)2 - 2αβ]/(αβ)2 ----(1)
In the quadratic equation ax2 + bx + c = 0,
sum of the roots = -b/a
product of the roots = c/a
α + β = -b/a
αβ = c/a
(1)----> -b/a = [(-b/a)2 - 2c/a]/(c/a)2
(-b/a) ⋅ (c2/a2) = b2/a2 - 2c/a
-bc2/a3 = b2/a2 - 2ac/a2
-bc2/a3 = (b2 - 2ac)/a2
-bc2 = a3 ⋅ [(b2 - 2ac)/a2]
-bc2 = a(b2 - 2ac)
-bc2 = ab2 - 2a2c
2a2c = ab2 + bc2
Divide both sides by a2c.
2 = b2/ac + bc/a2
So, the value of (b2/ac) + (bc/a2) is 2.
Problem 4 :
If L + M + N = 0 and L, M, N are rationales, examine the nature of the roots of the equation
(M + N - L)x2 + (N + L - M)x + (L + M - N) = 0
Solution :
Given : L + M + N = 0.
L + M = -N
M + N = -L
N + L = -M
Given : (M + N - L)x2 + (N + L - M)x + (L + M - N) = 0.
(-L - L)x2 + (-M - M)x + (-N - N) = 0
- 2Lx2 - 2Mx - 2N = 0
Divide both sides by -2.
Lx2 + Mx + N = 0
In the above quadratic equation a = L, b = M and c = N.
Substitute a = L, b = M and c = N in the discriminant of the quadratic equation (b2- 4ac).
b2- 4ac = M2 - 4LN
b2- 4ac = (-M)2 - 4LN
Substitute -M = L + N.
b2- 4ac = (L + N)2 - 4LN
b2- 4ac = L2 + N 2 + 2LN - 4LN
b2- 4ac = L2 + N 2 - 2LN
b2- 4ac = (L - N)2
Because b2-4ac > 0 and also a perfect square, the roots are real and rational.
Problem 5 :
If p ≠ q and p2 = 5p - 6, q2 = 5q - 6, find the quadratic equation having roots p/q and q/p.
Solution :
Given : p2 = 5p - 6 and q2 = 5q - 6.
p2 - 5p + 6 = 0 and q2 - 5q + 6 = 0
By solving the above quadratic equations, we get
p = -2, -3
q = -2, -3
Because p ≠ q, we can take p = -2 and q = -3.
p/q = -2/(-3) = 2/3
q/p = 3/2
Construction of quadratic equation :
x2 - (sum of the roots)x + product of the roots = 0
Quadratic equation having roots p/q and q/p :
x2 - (p/q + q/p)x + p/q ⋅ q/p = 0
x2 - (p/q + q/p)x + 1 = 0
Substitute p/q = 3/2 and q/p = 2/3.
x2 - (3/2 + 2/3)x + 1 = 0
x2 - (13/6)x + 1 = 0
Multiply both sides by 6.
6x2 - 13x + 6 = 0
Hence, the required quadratic equation is
6x2 - 13x + 6 = 0
Problem 6 :
If one root of the equation x2 - 8x + m = 0 exceeds the other by 4, then find the value of m.
Solution :
In the given equation x2 - 8x + m = 0, constant term m is positive.
The two factors of m must satisfy the following two conditions.
(i) Sum of the two factors of m must be equal to the middle term - 8.
(ii) One root of the equation must exceed the other by 4. That is, there must be a difference of 4 between the two roots.
The above two conditions can be met, only if the two factors of m are
- 2 and - 6
Then, we have
m = (- 2) ⋅ (- 6)
m = 12
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 143)
Apr 13, 25 12:01 PM
Digital SAT Math Problems and Solutions (Part - 143) -
Quadratic Equation Problems with Solutions
Apr 12, 25 08:21 PM
Quadratic Equation Problems with Solutions -
Digital SAT Math Problems and Solutions (Part - 142)
Apr 11, 25 06:26 PM
Digital SAT Math Problems and Solutions (Part - 142)