PROBLEMS ON SQUARES AND SQUARE ROOTS

Problem 1 :

Write the first five square numbers.

Solution :

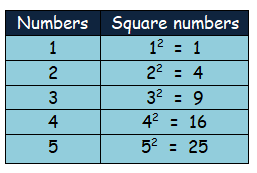
So, the first five square numbers are 1, 4, 9, 16, 25

Problem 2 :

The Square of 5.5 is   

Solution :

(5.5)²  =  (5.5) × (5.5)

=  30.25

Problem 3 :

The Square of 0.7 is

Solution :

(0.7)²  =  (0.7) × (0.7)

=  0.49

Problem 4 :

The Square of 500 will have _----------- zeroes.

Solution :

(500)²  =  (500) × (500)

=  250000

So, the Square of 500 has 4 zeroes.

Problem 5 :

The Square root of 24025 will have _--------- digits.

Solution :

Given, 24025

Number of digits  =  5 (odd)  = n

Number of digits  in the Square root =  (n + 1)/2

=  (5 + 1)/2

=  6/2

= 3

So, The Square root of 24025 has 3 digits.

Problem 6 :

Show that 500 is not a perfect square

Solution :

Using prime factorization method :

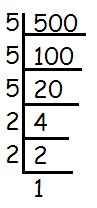
500  =  √(5 × 5 × 5 × 2 × 2)

Since there are not grouped in identical pairs, 500 is not a perfect square.

Problem 7 :

The digit at the ones place of 57² is               

Solution :

57²  =  57 x 57

=  3249

So, the digit at the ones place of 57² is 9.

Problem 8 :

There are _------- perfect squares between 1 and 100.

Solution :

The perfect squares between 1 and 100 is 4, 9, 16, 25, 36, 49, 64, and 81.

So, there are 8 perfect squares between 1 and 100.

Problem 9 :

The units digit in the square of 1294 is              

Solution :

By using the property of square numbers,

If a number has 4 or 6 in the unit's place then its square ends in 6.

1294  =  4²  =  16

So, the  units digit in the square of 1294 is always end with 6.

Problem 10 :

Check whether 90 is a perfect square or not by using prime factorization.

Solution :

Using prime factorization method :

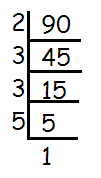
90  =  √(2 × 3 × 3 × 5)

Since there are not grouped in identical pairs, 90 is not a perfect square.

Problem 11 :

Using prime factorization, find the square roots of 11025

Solution :

Decompose 11025 into prime factors using synthetic division.

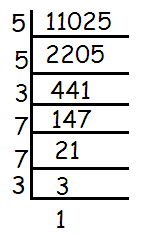
The square root of 11025  =  √(5 × 5 × 3 × 7 × 7 × 3)

Inside the radical sign, if the same number is repeated twice, take one number out of the radical sign.

  =  5 × 3 × 7

  =  105

So, the square root of 11025 is 105.

Problem 12 :

Using prime factorization, find the square roots of 4761

Solution :

Decompose 4761 into prime factors using synthetic division.

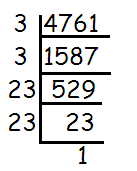
The square root of 4761  =  √(3 × 3 × 23 × 23)

Inside the radical sign, if the same number is repeated twice, take one number out of the radical sign.

=  3 × 23

=  69

So, the square root of 4761 is 69.

Problem 13 :

Find the least number of four digits that is a perfect square.

Solution :

The least number of four digits is 1000.

Using Long Division Method :

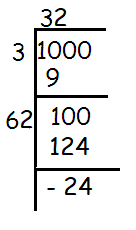
(32)² is more than 1000 by 24.

So, the least number to be added to 1000 is 24.

1000 + 24 =  1024

Therefore, the smallest four digit perfect square number is 1024.

Problem 14 :

Find the greatest number of three digits that is a perfect square.

Solution :

The Greatest number of three digits is 999.

Using Long Division Method :

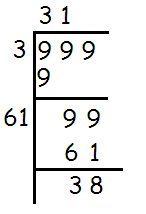
Since 999 is not a perfect square, now to find the largest 3 digits perfect square number subtract 38 from 999.

Required number  =   999 - 38

=  961

So, the greatest three digit perfect square number is 961.

Problem 15 :

Find the smallest perfect square divisible by 3, 4, 5 and 6.

Solution :

We are taking the  Least Common Multiple of 3, 4, 5 and 6

LCM of (3, 4, 5, 6)  =  2 × 2 × 3 × 5  

LCM  =  60

Since 3 and 5 are not identical pairs, we should multiple 3 and 5 by 60.

That is,

=  60 × 3 × 5

=  900

So, the required perfect square is 900

Problem 16 :

A number is 64 times of the square of its reciprocal. The number is :

a) 10      b) 4       c) 2       d) 16

Solution :

Let the required number be x. Its reciprocal will be 1/x.

A number = 64 times of the square of its reciprocal. So,

x = 64 (1/x²)

x³ = 64

x³ = 4³

x = 4

So, the required number is 4. Option b is correct.

Problem 17 :

The smallest perfect square number exactly divisible by 4, 5, 6, 15, 18 is

a) 800     b) 225     c) 361    d) 900

Solution :

Prime factors of 800 :

= 2⁵ x 5²

Here 2, 5, 10, 8, 20, ...... these are factors, since in this we cannot see 6 and 15 as factors. Then the required number is not 800.

Prime factors of 225 :

= 3² x 5²

3, 9, 15, 25, ........ are the factors but 18 and 4 are not factors. Then, the required number is not 225.

Prime factors of 361 :

= 19 x 19

From this, the required number is not 361.

Prime factors of 900 :

= 3² x 2² x 5²

From this, it is clear that 4, 5, 6, 15, 18 are factors. Then the required number is 900.

Problem 18 :

A gardener plants 17956 trees in such a way that there are as many rows as there are trees in each row. The number of trees in a row are

a) 136         b) 164      c) 134     d) 166

Solution :

Let x be the number of rows and x be the number of columns.

Total number of trees = x²

x² = 17956

x = √134 x 134

x = 134

So, there are 134 trees in each row and 134 rows are there.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.