THEORTICAL PROBABILITY EXAMPLE PROBLEMS

The theoretical probability of an event happening is based on what we expect to occur.

P(event happens)

=  number of ways the event can happen/total number of possible outcomes

Choosing blue bead from the jar.

Total number of beads  =  8

4 blue + 2 green + 1 yellow  =  8

P(Choosing blue bead)  =  number of blue beads / total number of beds

=  4/8

=  1/2

Problem 1 :

A die is rolled. What is the theoretical probability of getting :

a) a "six"

b) a "prime number"?

Solution :

The possible outcomes are

1, 2, 3, 4, 5 and 6

(a)  P(a ‘six’) = 1/6

b) The possible ‘prime’ number outcomes are : 2, 3 and 5.

P(a ‘prime’) = 3/6 (or) 1/2

Problem 2 :

A bag contains 1 yellow, 2 green and 5 blue beds. One bead is chosen at random. Find the probability that it is :

(a)  Yellow  (b)  not yellow

Solution :

Total number of beads  =  8

4 blue + 2 green + 1 yellow  =  8

(a)  P(getting yellow)  =  1/8

(b)  P(not getting yellow)  =  1 - (1/8)

=  7/8

Problem 3 :

1 A die numbered 1 to 6 is rolled once. Find:

a) P(3)

b) P(even number)

c) P(a number at least 1)

d) P(5)

e) P(not a 5)

f) P(a number greater than 6)

Solution :

Possible outcomes are 

1, 2, 3, 4, 5, 6

a)  P(getting 3)  =  1/6

b)  P(getting even number)  =  3/6 (or) 1/2

c)  P(atleast 1)  =  6/6  =  1

d)  P(5)  =  1/6

e)  P(not 5)  =  5/6

f) P(a number greater than 6)

Since it is a impossible event, the answer is 0.

Problem 4 :

The five illustrated cards are well shuffled and placed face down on a table. One of the cards is randomly chosen. 

Find:

a) P(A)

b) P(C)

c) P(not C)

d) P(A or B)

Solution :

Total number of cards  =  5

2 A's + 2 B's + 1 C  =  5

a)  P(getting card of A)  =  2/5

b)  P(getting card of C)  =  1/5

c)  P(not C)  =  4/5

d)  P(A or B)  =  4/5

Problem 5 :

A bag contains 10 beads. 5 are white, 2 are red, 1 is blue, 1 is green and 1 is black. A bead is taken at random from the bag. Find:

a) P(white)

b) P(blue)

c) P(not black)

Solution :

Total number of beads 

5 white + 2 red + 1 blue + 1 green + 1  black  =  10

=  5 + 2 + 1 + 1 + 1

=  10

a) P(white)

=  Number of white beads/total number of beads

=  5/10

=  1/2

b) P(blue)

=  Number of blue beads/total number of beads

=  1/10

c) P(not black)

=  Number of beads that are not black/total number of beads

=  (5+2+1+1)/10

=  9/10

Problem 6 :

A letter is randomly chosen from GENEVA.

a)  Find the probability that it is:

(i) an E

(ii) a Z

b) Given that the letter chosen first is a G and it is removed, what is the probability that a second randomly chosen letter is a vowel?

Solution :

Total number of letters  =  G, E, N, E, V, A

=  6

(i)  P(selecting E)  =  2/6

=  1/3

(ii)  P(selecting Z) :

Since it is impossible event, the required probability is 0.

(b)  After removing G, the total number of letter is 5.

Selecting E and A can be considered as vowel.

=  3/5

Problem 7 :

A dart board has 30 sectors, numbered 1 to 30. A dart is thrown towards the bulls-eye and misses in a random direction. Determine the probability that the dart hits:

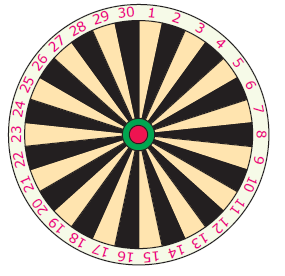
a) a multiple of 5

b) a number between 7 and 13 inclusive

c) a number greater than 18

d) 15

e) a multiple of 7

f) an even number that is a multiple of 3.

Solution :

Total number of terms  =  30

(a)  Multiple of 5 are

5, 10, 15, 20, 25, 30

P(Multiple of 5)  = 6/30

=  1/5

b) a number between 7 and 13 inclusive

7, 8, 9, 10, 11, 12, 13

P(getting 7 and 13 inclusive)  =  7/30

c) a number greater than 18

19, 20, 11, 12, 13, ............30

P(a number greater than 18)  =  11/30

d) 15

P(getting 15)  =  1/30

e) a multiple of 7

7, 14, 21, 28

P(a multiple of 7)  =  4/30

=  2/15

f) an even number that is a multiple of 3.

Multiple of 3 : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30

Even number multiple of 3 : 6, 12, 18, 24, 30

P(an even number that is a multiple of 3)  =  5/30

=  1/6

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.