PROBLEMS ON TRIANGLES FOR SAT PRACTICE

Problem 1 :

In ΔABC shown below, AB = BC, m∠BCD = 110° and m∠BDE = 140°. Find m∠1, m∠2, m∠3 and m∠4.

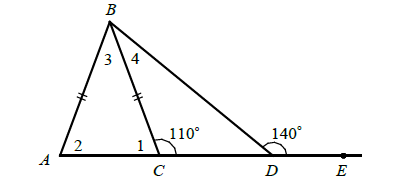
Solution :

Since AB = BC, m∠1 = m∠2.

From the figure above,

m∠ACB + m∠BCD = 180°

m∠1 + 110 = 180°

m∠1 = 70°

m∠2 = 70°

In triangle ABC,

m∠1 + m∠2 + m∠3 = 180°

70° + 70° + m∠3 = 180

m∠3 = 180° - 140°

m∠3 = 40°

m∠CDB + m∠BDE = 180°

m∠CDB + 140° = 180°

m∠CDB = 40°

m∠BCD + m∠CDB + m∠DBC = 180°

110° + 40° + m∠4 = 180°

m∠4 = 180° - 150°

m∠4 = 30°

Problem 2 :

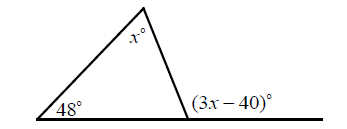
In the triangle shown above, what is the value of x?

Solution :

By Exterior Angle Theorem,

x° + 48° = (3x - 40)°

x + 48 = 3x - 40

-2x = -88

x = 44

Problem 3 :

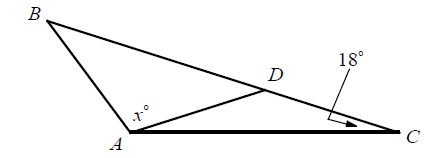
In ΔABC ABC shown above, if AB = AD = DC, what is the value of x?

Solution :

In triangle ADC,

m∠DCA = 18°

m∠CAD = 18°

By Exterior Angle Theorem,

m∠ADB = m∠DAC + m∠DCA

m∠ADB = 18° + 18°

m∠ADB = 36°

Since AD = AB,

m∠ADB = m∠ABD = 36°

In triangle ABC,

m∠ABC + m∠BAC + m∠ACB = 180

36° + x° + 18° + 18° = 180°

36 + 36 + x = 180

x = 180 - 72

x = 108

Problem 4 :

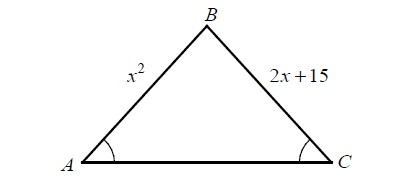
In ΔABC shown above, m∠A = m∠C. If x > 0, what is the value of x?

Solution :

It is isosceles triangle,

AB = BC

x² = 2x + 15

x² - 2x - 15 = 0

(x - 5)(x + 3) = 0

x - 5 = 0  or  x + 3 = 0

x = 5  or  x = -3

Since x > 0, the value of x is 5.

Problem 5 :

In the figure above AC is perpendicular to BC. What is the measure of m∠ABC?

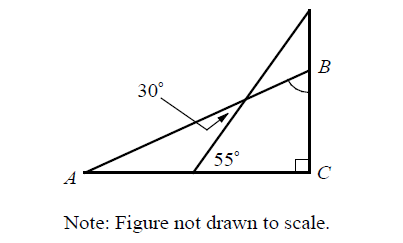
Solution :

By Exterior Angle Theorem,

m∠A + 30° = 55°

m∠A = 25°

In triangle ABC,

m∠BAC + m∠ACB + m∠ABC = 180

25° + 90° + m∠ABC = 180°

115° + m∠ABC = 180°

m∠ABC = 180° - 115°

m∠ABC = 65°

Problem 6 :

In the figure above, AD = BD = BC. If m∠A = 26°. What is the measure of m∠DBC?

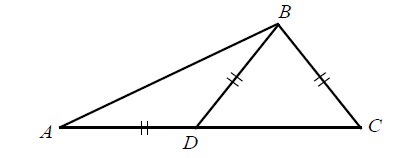
Solution :

In triangle ABD, since AD = BD,

m∠A = m∠ABD = 26°

By Exterior Angle Theorem,

m∠BDC = m∠A + m∠ABD

m∠BDC = 26° + 26°

m∠BDC = 52°

In triangle BDC, since BD = BC, 

m∠BDC = m∠BCD = 52°

And also,

m∠BDC + m∠BCD + m∠CBD = 180°

52° + 52° + m∠CBD = 180°

104° + m∠CBD = 180°

m∠CBD = 180° - 104°

m∠CBD = 76°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.