PROBLEMS ON TRIGONOMETRIC RATIOS

Problem 1 :

For the measures in the figure shown below, compute sine, cosine and tangent ratios of the angle θ.

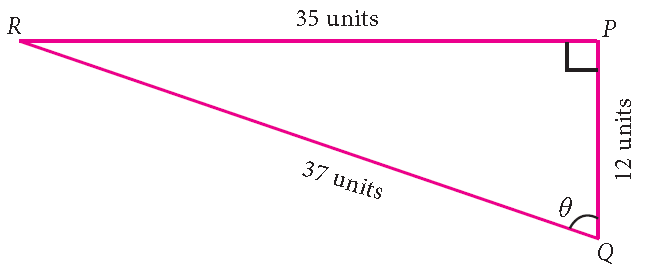
Solution :

In the given right angled triangle, note that for the given angle θ, PR is the ‘opposite’ side and PQ is the ‘adjacent’ side.

Then, 

sin θ  =  opposite side / hypotenuse  =  PR/QR  =  35/37

cos θ  =  adjacent side / hypotenuse  =  PQ/QR  =  12/37

tan θ  =  opposite side / adjacent side  =  PR/PQ  =  35/12

Problem 2 :

Find the six trigonometric ratios of the angle θ using the diagram shown below. 

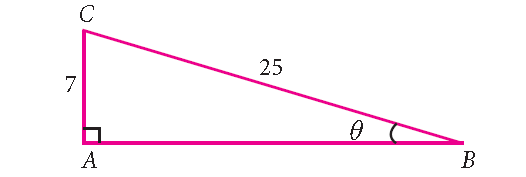
Solution :

In the given right angled triangle, note that for the given angle θ, AC is the ‘opposite’ side and AB is the ‘adjacent’ side.

And also, the length of the adjacent side 'AB' is not given. 

Find the length of AB. 

By Pythagorean Theorem,

BC²  =  AB² + AC²

25²  =  AB² + 7²

625  =  AB² + 49

Subtract 49 from each side. 

576  =  AB²

24²  =  AB²

24  =  AB  

Then, 

sin θ  =  opposite side / hypotenuse  =   AC/ BC  =  7/25

cos θ  =  adjacent side / hypotenuse  =  AB/BC  =  24/25

tan θ  =  opposite side / adjacent side  =  AC/AB  =  7/24

csc θ  =  1 / sin θ  =  25/7

sec θ  =  1 / cos θ  =  25/24

cot θ  =  1 / tan θ  =  24/7

Problem 3 :

If tan A  =  2/3, then find all the other trigonometric ratios. 

Solution : 

tan A  =  opposite side / adjacent side  =  2 / 3

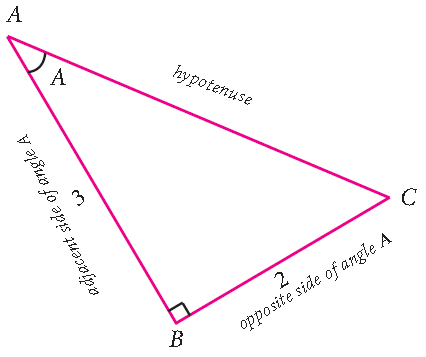
By Pythagorean Theorem,

AC²  =  AB² + BC²

AC²  =  3² + 2²

AC²  =  9 + 4

AC²  =  13

AC  =  √13

Then, 

sin A  =  opposite side / hypotenuse  =   BC/ AC  =  2/√13

cos A  =  adjacent side / hypotenuse  =  AB/AC  =  3/√13

csc A  =  1 / sin A  =  √13/2

sec A  =  1 / cos A  =  √13/3

cot A  =  1 / tan A  =  3/2

Problem 4 :

If sec θ  =  2/3, then find the value of

(2sin θ - 3cos θ) / (4sin θ - 9cos θ) 

Solution : 

sec θ  =  hypotenuse / adjacent side  =  13 / 5

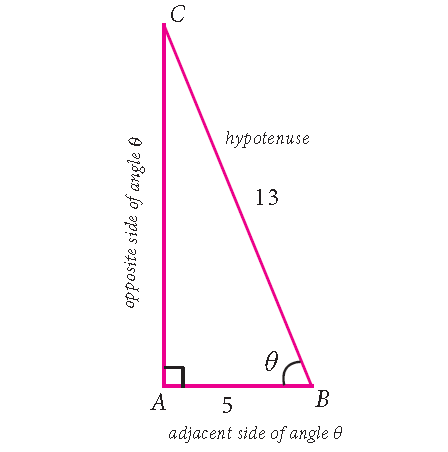
By Pythagorean Theorem,

BC²  =  AB² + AC²

13²  =  5² + AC²

169  =  25 + AC²

Subtract 25 from each side. 

144  =  AC²

12²  =  AC²

12  =  AC

Then, 

sin θ  =  opposite side / hypotenuse  =   AC/BC  =  12/13

cos θ  =  adjacent side / hypotenuse  =  AB/BC  =  5/13

(2sin θ - 3cos θ) / (4sin θ - 9cos θ) : 

=  (2 ⋅ 12/13 - 3 ⋅ 5/13) / (4 ⋅ 12/13 - 9 ⋅ 5/13)

=  (24/13 - 15/13) / (48/13 - 45/13)

=  [(24 - 15)/13] / [(48 - 45)/13]

=  (9/13) / (3/13)

=  (9/13) ⋅ (13/3)

=  9/3

=  3

So, 

(2sin θ - 3cos θ) / (4sin θ - 9cos θ)   =  3

To learn SOHCAHTOA in detail,

Please click here

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

If you have any feedback about our math content, please mail us : 

v4formath@gmail.com

We always appreciate your feedback. 

You can also visit the following web pages on different stuff in math. 

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractrions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6