PROOF AND PERPENDICULAR LINES

Types of Proofs

(i) Two - Column Proof :

This is the most formal type of proof. It lists numbered statements in the left column and a reason for each statement in the right column.

(ii) Paragraph Proof :

This is the most formal type of proof. It lists numbered statements in the left column and a reason for each statement in the right column.

(ii) Flow Proof :

This type of proof uses the same statements and reasons as a two-column proof, but the logical flow connecting the statements is indicated by arrows.

Results about Perpendicular Lines

Result 1 :

If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular.

The diagram given below illustrates this.

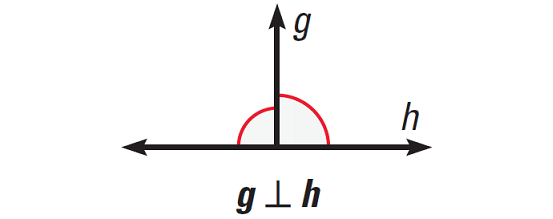
Result 2 :

If two sides of two adjacent acute angles are perpendicular, then the angles are complementary.

The diagram given below illustrates this.

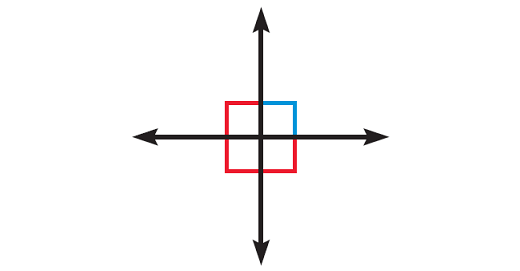
Result 3 :

If two lines are perpendicular, then they intersect to form four right angles.

The diagram given below illustrates this.

Example 1 :

In the diagram given below,

∠5 and ∠6 are a linear pair

∠6 and ∠7 are a linear pair

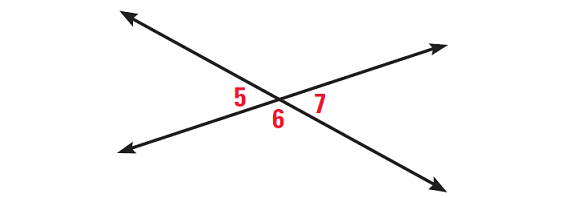
Prove ∠5 ≅ ∠7 using two-column proof, paragraph proof and flow proof.

Solution :

Two-column Proof :

Paragraph Proof :

Because ∠5 and ∠6 are a linear pair, the linear pair postulate says that ∠5 and ∠6 are supplementary. The same reasoning shows that ∠6 and ∠7 are supplementary. Because ∠5 and ∠7 are both supplementary to ∠6, the congruent supplements theorem says that ∠5 ≅ ∠7.

Flow Proof :

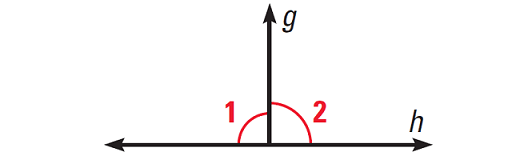
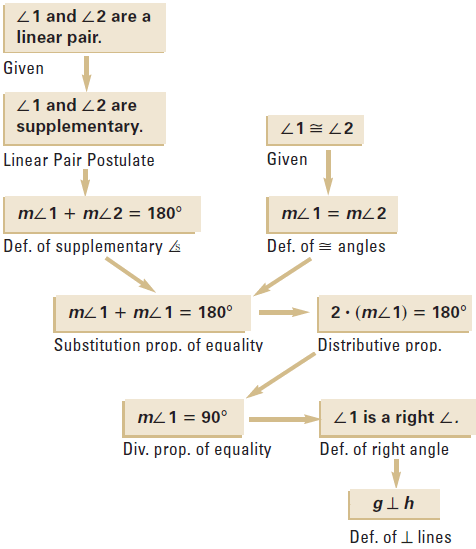
Example 2 :

In the diagram given below, ∠1 and ∠2 are congruent and also a linear pair. Using flow proof, prove that the lines g and h are perpendicular.

Solution :

Example 3 :

If two sides of the adjacent acute angles (2x + 3)° and (4x - 6)° are perpendicular, find the value of x. 

Solution :

According to result 2, if two sides of two adjacent acute angles are perpendicular, then the angles are complementary.

So, we have 

(x+3)° + (2x-6)°  =  90°

x + 3 + 2x - 6  =  90 

Simplify. 

3x - 3  =  90

Add 3 to both sides. 

3x  =  93

Divide both sides by 3. 

x  =  31

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.