PROOF BY VENN DIAGRAM
Here we are going to see the proof of properties of sets operations and De Morgan's laws by Venn diagram.
The following are the important properties of set operations.
(i) Commutative Property :
AuB = BuA (Set union is commutative)
AnB = BnA (Set intersection is commutative)
(ii) Associative Property :
Au(BuC) = (AuB)uC (Set union is associative)
An(BnC) = (AnB)nC (Set intersection is associative)
(iii) Distributive Property :
An(BuC) = (AnB)u(AnC)
(Intersection distributes over union)
Au(BnC) = (AuB)n(AuC)
(Union distributes over intersection)
De Morgan's law for set difference :
For any three sets A, B and C, we have
A\(BuC) = (A\B)n(A\C)
A\(BnC) = (A\B)u(A\C)
De Morgan's law for set complementation :
Let U be the universal set containing sets A and B. Then
(AuB)' = A'nB'
(AnB)' = A'uB'
Properties of Set Operations - Proof by Venn Diagram
Problem 1 :
A = {-10, 0, 1, 9, 2, 4, 5}
B = {-1, -2, 5, 6, 2, 3, 4}
For the sets A and B above, verify that
(i) Set union is commutative. Also verify it by using Venn diagram.
(ii) Set intersection is commutative. Also verify it by using Venn diagram.
Solution :
(i) Let us verify that set union is commutative.
AuB = {-10, 0, 1, 9, 2, 4, 5} u {-1, -2, 5, 6, 2, 3, 4}
AuB = {-10, -2, -1, 0, 1, 2, 3, 4, 5, 6, 9} ----(1)
BuA = {-1, -2, 5, 6, 2, 3, 4 } u { -10, 0, 1, 9, 2, 4, 5}
BuA = { -10, -2, -1, 0, 1, 2, 3, 4, 5, 6, 9} ----(2)
From (1) and (2),
AuB = BuA
By Venn diagram,
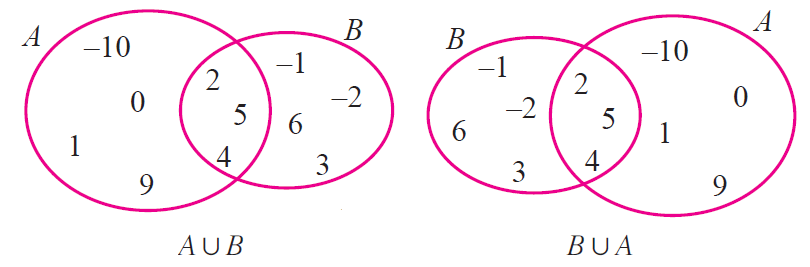
From the above two Venn diagrams, it is clear that
AuB = BuA
Hence, it is verified that set union is commutative.
(ii) Let us verify that set intersection is commutative.
AnB = {-10, 0, 1, 9, 2, 4, 5} n {-1, -2, 5, 6, 2, 3, 4}
AnB = {2, 4, 5} ----(1)
BnA = {-1, -2, 5, 6, 2, 3, 4} u {-10, 0, 1, 9, 2, 4, 5}
BnA = {2, 4, 5} ----(2)
From (1) and (2),
AnB = BnA
By Venn diagram,
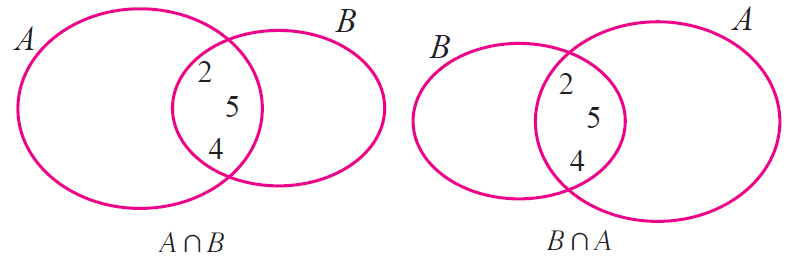
From the above two Venn diagrams, it is clear that
AnB = BnA
Hence, it is verified that set intersection is commutative.
Problem 2 :
A = {1, 2, 3, 4, 5}
B = {3, 4, 5, 6}
C = {5, 6, 7, 8}
For the three sets A, B and C above, verify that
Au(BuC) = (AuB)uC
Also verify it by using Venn diagram.
Solution :
Let us verify that set union is associative.
BuC = {3, 4, 5, 6} u {5, 6, 7, 8}
BuC = {3, 4, 5, 6, 7, 8}
Au(BuC) = {1, 2, 3, 4, 5} u {3, 4, 5, 6, 7, 8}
Au(BuC) = {1, 2, 3, 4, 5, 6, 7, 8} ----(1)
AuB = {1, 2, 3, 4, 5} u {3, 4, 5, 6}
AuB = {1, 2, 3, 4, 5, 6}
(AuB)uC = {1, 2, 3, 4, 5, 6} u {5, 6, 7, 8}
(AuB)uC = {1, 2, 3, 4, 5, 6, 7, 8} ----(2)
From (1) and (2),
Au(BuC) = (AuB)uC
By Venn diagram,
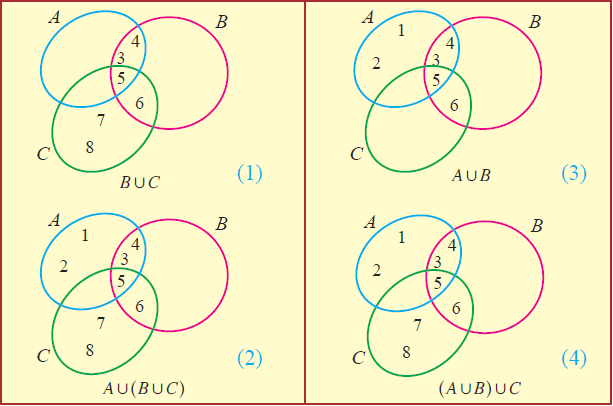
From the above Venn diagrams (2) and (4), it is clear that
Au(BuC) = (AuB)uC
Hence, it is verified that set union is associative.
Problem 3 :
A = {a, b, c, d}
B = {a, c, e}
C = {a, e}
For the three sets A, B and C above, verify that
An(BnC) = (AnB)nC
Also verify it by using Venn diagram.
Solution :
Let us verify that set intersection is associative.
BnC = {a, c, e} u {a, e}
BnC = {a, e}
An(BnC) = {a, b, c, d} n {a, e}
An(BnC) = {a} ----(1)
AnB = {a, b, c, d} u {a, c, e}
AnB = {a, c}
(AnB)nC = {a, c} n {a, e}
(AnB)nC = {a} ----(2)
From (1) and (2),
An(BnC) = (AnB)nC
By Venn diagram,
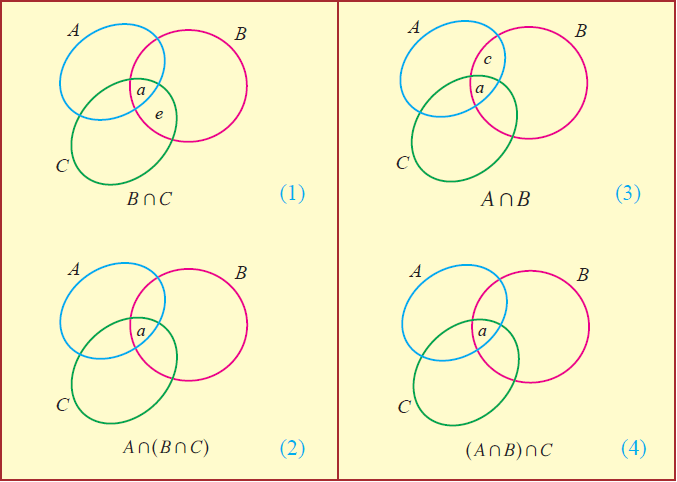
From the above Venn diagrams (2) and (4), it is clear that
An(BnC) = (AnB)nC
Hence, it is verified that set intersection is associative.
Problem 4 :
A = {0, 1, 2, 3, 4}
B = {1, -2, 3, 4, 5, 6}
C = {2, 4, 6, 7}
For the three sets A, B and C above, verify that
Au(BnC) = (AuB)n(AuC)
Also verify it by using Venn diagram.
Solution :
Let us verify that union distributes over intersection.
BnC = {1, -2, 3, 4, 5, 6} n {2, 4, 6, 7}
BnC = {4, 6}
Au(BnC) = {0, 1, 2, 3, 4} u {4, 6}
Au(BnC) = {0, 1, 2, 3, 4, 6} ----(1)
AuB = {0, 1, 2, 3, 4} u {1, -2, 3, 4, 5, 6}
AuB = {-2, 0, 1, 2, 3, 4, 5, 6}
AuC = {0, 1, 2, 3, 4} u {2, 4, 6, 7}
AuC = {0, 1, 2, 3, 4, 6, 7}
(AuB)n(AuC) = {-2, 0, 1, 2, 3, 4, 5, 6} n {0, 1, 2, 3, 4, 6, 7}
(AuB)n(AuC) = {0, 1, 2, 3, 4, 6} ----(1)
From (1) and (2),
Au(BnC) = (AuB)n(AuC)
By Venn diagram,

From the above Venn diagrams (2) and (5), it is clear that
Au(BnC) = (AuB)n(AuC)
Hence, it is verified that union distributes over intersection.
De Morgan's Law for Set Difference - Proof by Venn Diagram
A\(BnC) = (A\B)u(A\C)
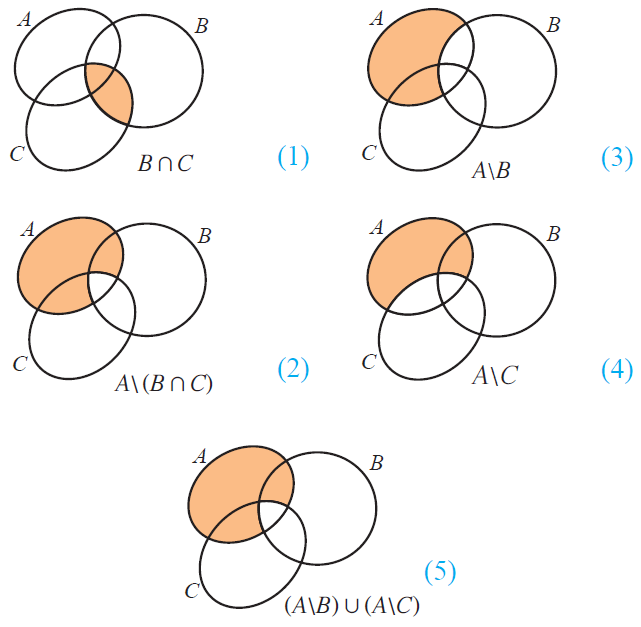
From the above Venn diagrams (2) and (5), it is clear that
A\(B n C) = (A\B)u(A\C)
Hence, De Morgan's law for set difference is verified.
Similarly, we can prove A\(BuC) = (A\B)n(A\C).
De Morgan's Law for Set Complementation - Proof by Venn Diagram
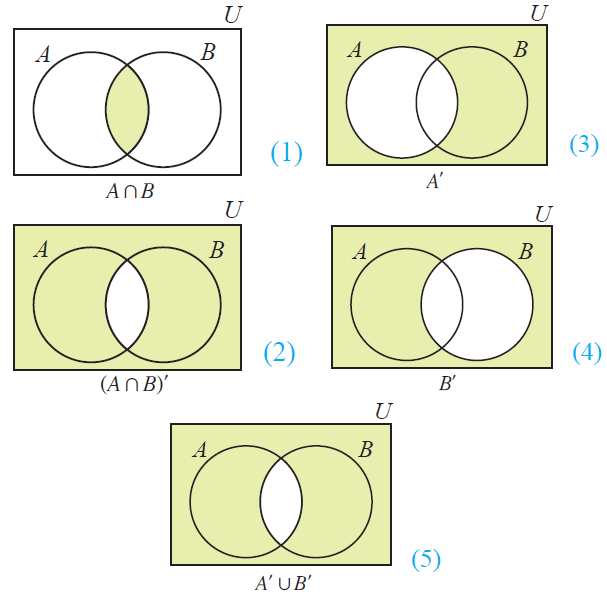
From the above Venn diagrams (2) and (5), it is clear that
(AnB)' = A'uB'
Hence, De Morgan's law for complementation is verified.
Similarly, we can prove (AuB)' = A'nB'.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 146)
Apr 18, 25 06:52 AM
Digital SAT Math Problems and Solutions (Part - 146) -
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145)

