PROPERTIES OF CHORD OF A CIRCLE

Property 1 :

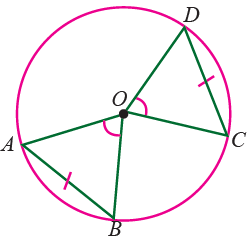
Equal chords of a circle subtend equal angles at the centre.

<AOB = <DOC

Property 2 :

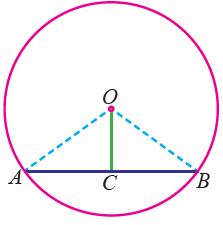
Perpendicular from the centre of a circle to a chord bisects the chord.

AC = BC

Property 3 :

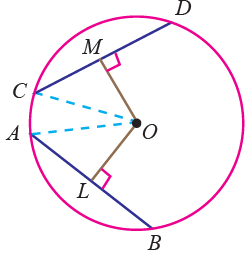
Equal chords of a circle are equidistant from the centre.

OM = OL

Property 4 :

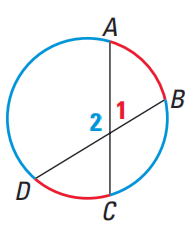
If two chords intersect inside a circle, then the measure of each angle formed is one half the sum of the measures of the arcs intercepted by the angle and its vertical angle.

m<1 = (1/2) (Measure arcCD+measure of arcAB)

m<2 = (1/2) (Measure arcBC+measure of arcCD)

Property 5 :

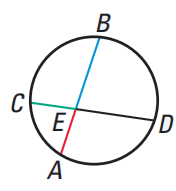
If two chords intersect inside a circle, then the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord.

EA ⋅ EB = EC ⋅ ED

Equal Chords of a Circle Subtend Equal Angles at the Center

Equal chords of a circle subtend equal angles at the centre.

chord AB = chord CD (<AOB = <COD)

Converse of the Result :

If the angles subtended by two chords at the centre of a circle are equal, then the chords are equal.

<AOB = <COD (chord AB = chord CD)

Perpendicular from the Center of a Circle to a Chord Bisects the Chord

Theorem 1 :

Perpendicular from the center of a circle to a chord bisects the chord.

Given : A circle with centre O and AB is a chord of the circle other than the diameter and OC ⊥ AB

To prove : AC = BC

Construction : Join OA and OB

Proof :

In triangles OAC and OBC

(i) OA = OB

(Radii of the same circle)

(ii) OC is common

(iii) <OCA = <OCB (Each 90°, since OC ⊥ AB)

(iv) Triangle OAC ≡ Triangle OBC

(RHS congruency.)

Hence, AC = BC

Converse of Theorem 1 :

The line joining the center of the circle and the midpoint of a chord is perpendicular to the chord.

Equal Chords of a Circle are Equidistant from the Center

Theorem 2 :

Equal chords of a circle are equidistant from the center.

Given : A circle with center O and radius r such that

chord AB = chord CD.

To prove : OL = OM

Construction :

Draw OL = AB and OM = CD. Join OA and OC

Proof :

(i) AL = (1/2) AB and CM = (1/2) CD

(Perpendicular from the centre of a circle to the chord bisects the chord.)

AB = CD (1/2) AB = (1/2) CD ==> AL = CM

(ii) OA = OC (radii)

(iii) <OMC= <OLA (Each 90°)

(iii) Triangle OLA ≡ Triangle OMC (RHS congruence.)

OL = OM

Hence AB and CD are equidistant from O .

Converse of Theorem 2 :

The chords of a circle which are equidistant from the center are equal.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

PROPERTIES OF CHORD OF A CIRCLE

Equal Chords of a Circle Subtend Equal Angles at the Center

Perpendicular from the Center of a Circle to a Chord Bisects the Chord

Equal Chords of a Circle are Equidistant from the Center

Recent Articles

Trigonometry Even and Odd Iidentities

SOHCAHTOA Worksheet

Trigonometry Pythagorean Identities