PROPERTIES OF CONGRUENT TRIANGLES WORKSHEET

1.  Prove the Reflexive Property of Congruent Triangles.

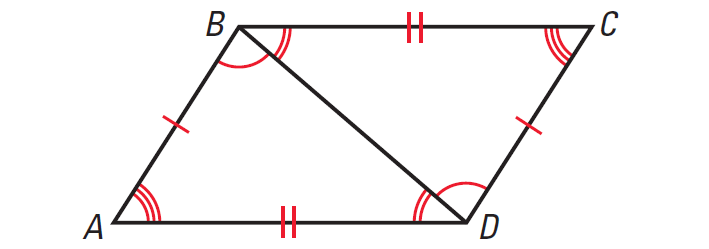
2.  In the diagram given below, triangle ABD is congruent to triangle BCD. Is triangle BCD congruent to triangle ABC ? Explain your reasoning. 

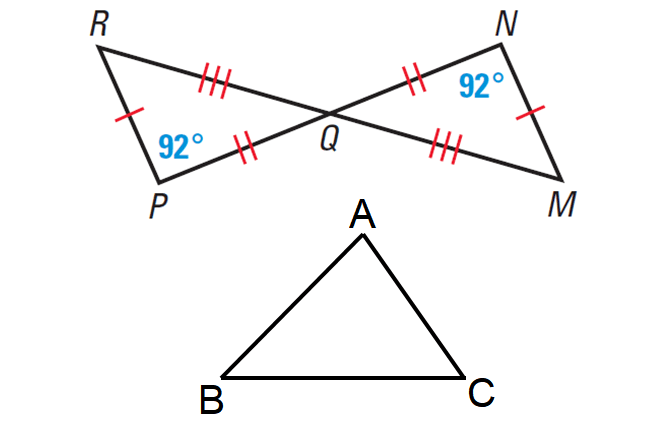
3.  In the diagram given below, Triangle MQN is congruent to triangle ABC. Prove that triangle PQR is congruent to triangle ABC. 

1. Answer :

If two triangle are considered to be congruent, they have to meet the following two conditions.

1. They must have exactly the same three sides.

2. They must have exactly the same three angles.

Every triangle and itself will meet the above two conditions. 

So, every triangle is congruent to itself.

2. Answer :

Yes, triangle BCD is congruent to triangle ABC. 

By Symmetry Property of Congruent Triangles, 

if ΔABD  ≅  ΔBCD, then 

ΔBCD  ≅  ΔABD. 

Thus, triangle BCD is congruent to triangle ABC.

3. Answer :

Given : Triangle MQN is congruent to triangle ABC.

In the above diagram, we do not have any details about the triangle ABC.

So, if we prove triangle PQR is congruent to MQN, then we can prove triangle PQR is congruent to triangle ABC using transitive property of congruent triangles.

Proving triangle PQR is congruent to triangle MQN :

From the above diagram, we are given that all three pairs of corresponding sides of triangle PQR and MQN are congruent. 

That is

RP ≅ MN, PQ ≅ NQ and QR ≅ QM

Because ∠P and ∠N have the same measure, ∠P ≅ ∠N.

By the Vertical Angles Theorem, we know that 

ΔPQR  ≅  ΔMQN

By the Third Angles Theorem, if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.

So, we have 

∠R  ≅  ∠M

So, all three pairs of corresponding sides and all three pairs of corresponding angles are congruent. By the definition of congruent angles, 

ΔPQR  ≅  ΔMQN

Using Transitive Property of Congruent Triangles :

By Transitive property of congruent triangles, 

if ΔPQR  ≅  ΔMQN and ΔMQN  ≅  ΔABC, then 

ΔPQR  ≅  ΔABC

Thus, triangle PQR is congruent to triangle ABC. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.