PROPERTIES OF CORRELATION COEFFICIENT

Property 1 :

The Coefficient of Correlation is a unit-free measure.

This means that if x denotes height of a group of students expressed in cm and y denotes their weight expressed in kg, then the correlation coefficient between height and weight would be free from any unit.

Property 2 :

The coefficient of correlation remains invariant under a change of origin and/or scale of the variables under consideration depending on the sign of scale factors.

This property states that if the original pair of variables x and y is changed to a new pair of variables u and v by effecting a change of origin and scale for both x and y i.e.

u  =  (x - a) / b

v  =  (y - c) / d

where a and c are the origins of x and y and b and d are the respective scales and then we have

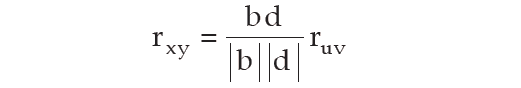
r_xy and rᵤᵥ being the coefficient of correlation between x and y and u and v respectively, From the result given in the above picture, numerically, the two correlation coefficients remain equal and they would have opposite signs only when b and d, the two scales, differ in sign.

Property 3 :

The coefficient of correlation always lies between –1 and 1, including both the limiting values i.e.

That is, 

-1  ≤  r  ≤  1

Property 4 : 

Correlation coefficient measuring a linear relationship between the two variables indicates the amount of variation of one variable accounted for by the other variable.

A better measure for this purpose is provided by the square of the correlation coefficient, known as ‘coefficient of determination’. This can be interpreted as the ratio between the explained variance to total variance i.e.

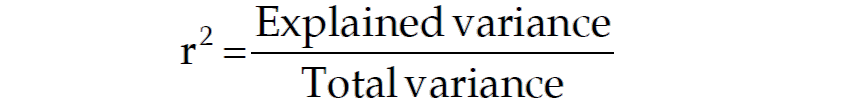
Thus a value of 0.6 for r indicates that (0.6)² × 100% or 36 per cent of the variation has been accounted for by the factor under consideration and the remaining 64 per cent variation is due to other factors.

The ‘coefficient of non-determination’ is given by (1–r²) and can be interpreted as the ratio of unexplained variance to the total variance.

Therefore, 

Coefficient of non-determination  =  (1 – r²) 

Practice Problems

Problem 1  :

Given that the correlation coefficient between x and y is 0.8, write down the correlation coefficient between u and v where

2u + 3x + 4  =  0

4v + 16x + 11  =  0

Solution : 

2u + 3x + 4  =  0

u  =  (-2) + (-3/2)x

scale  =  -3/2

And 

4v + 16x + 11  =  0

v  =  (-11/4) + (-4)y

scale  =  -4 

In both the equations, the sign of scales is same. That is "negative". 

Therefore, 

Correlation coefficient of 'uv' is

=  Correlation coefficient of 'xy'

Correlation coefficient of 'uv'  =  0.8

Problem 2  :

Given that the correlation coefficient between x and y is 0.8, write down the correlation coefficient between u and v where

2u – 3x + 4  =  0

4v + 16x + 11  =  0

Solution : 

2u – 3x + 4  =  0

u  =  (-2) + (3/2)x

scale  =  3/2 

And 

4v + 16x + 11  =  0

v  =  (-11/4) + (-4)y

scale  =  -4 

In the above two equations, the sign of scales are different. That is "positive" and "negative" 

Therefore, 

Correlation coefficient of 'uv' is

=  - correlation coefficient of 'xy' 

Correlation coefficient of 'uv'  =  - 0.8

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.