PROPERTIES OF DEFINITE INTEGRALS WITH EXAMPLES

Property 1 :

Integration is independent of change of variables provided the limits of integration remain the same.

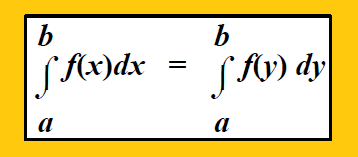
Property 2 :

If the limits of definite integral are interchanged, then the value of integral changes its sign only.

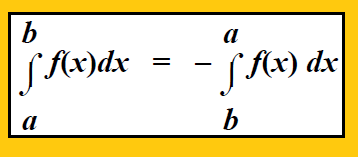
Property 3 :

Property 4 :

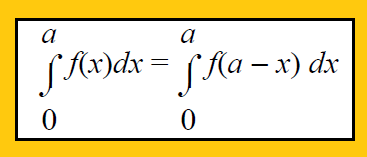
Property 5 :

If f(x) is integrable on a closed interval containing the three numbers a, b and c, then regardless of the order of a, b and c.

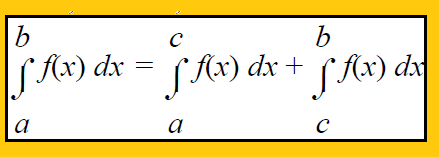
Property 6 :

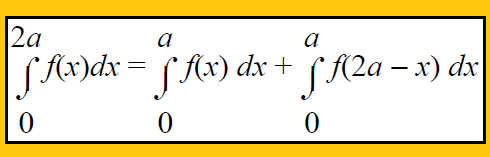
Property 7 :

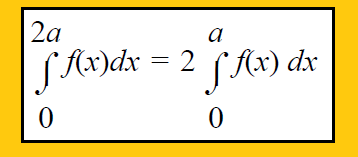
Property 8 :

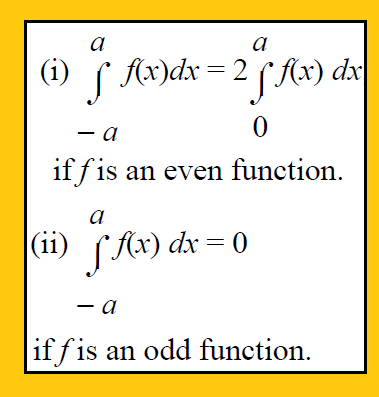
Examples on Properties of Integrals

Example 1 :

Evaluate 

Solution :

Since the upper and lower limit they are numerically equal and signs alone different, we have to check if the given function is odd or even.

Let f(x) = x³ sin²x

To find f(-x), we have to apply -x for x. So,

f(-x) = (-x)³ [sin (-x)]²

= -x³ [-sin x]²

f(-x) = -x³ [sin² x]

It is proved that f(-x) = -f(x)

Then it is odd function. 

Example 2 :

Solution :

Since the upper and lower limit they are numerically equal and signs alone different, we have to check if the given function is odd or even.

Let f(x) = log [(3 - x) / (3 + x)]

Put x = -x

f(-x) = log [(3 - (-x)) / (3 + (-x))]

= log [(3 + x) / (3 - x)]

= log (3 + x) - log (3 - x)]

= log (3 + x) - log (3 - x)

= -[ log (3 - x) - log (3 + x)]

= -[log (3 - x)/(3 + x)]

f(-x) = -f(x)

So, it is odd function.

Example 3 :

Solution :

Let f(x) = x sin x

Put x = -x

f(-x) = -x sin (-x)

= x sin x

f(-x) = f(x)

So, it is even function.

u = x, dv = sin x

u'= 1 and v = -cos x

Example 4 :

Solution :

Let f(x) = sin² x

Put x = -x

f(-x) = [sin(-x)]²

= sin² x

f(-x) = f(x)

So, it is even function.

Example 5 :

Solution :

Example 6 :

Solution :

Example 7 :

Solution :

Example 8 :

Given that

find the following

Solution :

i)  

= 10 + 3

= 13

ii)  

iii)

iv)

= 3(10)

= 30

Example 9 :

The graph of g(x)  is shown. Evaluate each integral by interpreting it in terms of areas.

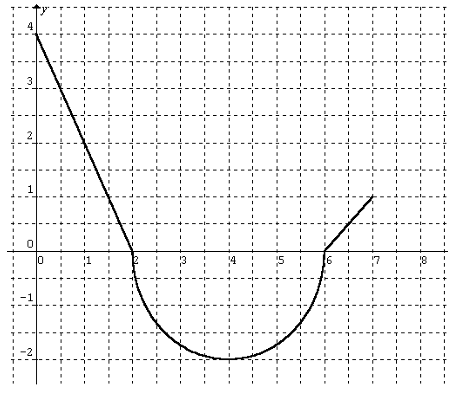
i)  

ii)  

iii)

Solution :

i)

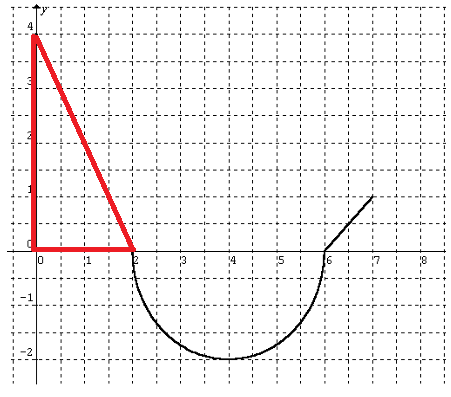
In between the interval 0 and 2, we see the triangle

Area of triangle = (1/2) x base x height

By observing the triangle, base = 2, height = 4

= (1/2) x 2 x 4

= 4 square units.

ii) 

In between the interval 2 and 6, we see the shape semicircle.

Area of semicircle = (1/2) πr²

Diameter = 4 units, radius = 2

= (1/2) π(2)²

= 2π square units

Since the portion lies below the x-axis,

iii) 

By observing the curve in between 6 to 7, we see the shape triangle.

Area of triangle = (1/2) x base x height

By observing the triangle, base = 1, height = 1

= (1/2) x 1 x 1

= 0.5 square units.

= 4.5 - 2(3.14)

= 4.5 - 6.28

= -1.78

Example 10 :

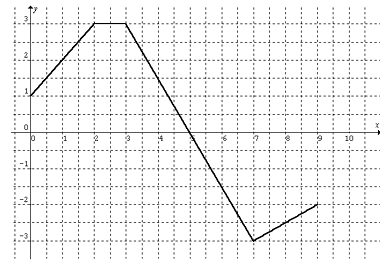
The graph of f(x)  is shown. Evaluate each integral by interpreting it in terms of areas.

i) 

ii)  

iii)  

iv)  

Solution :

i) 

By observing the figure from 0 to 2, we see the shape called trapezium.

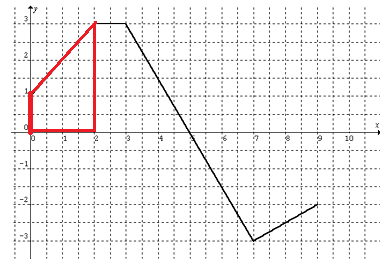
Area of trapezium = (1/2) x h (a + b)

Here a and b are parallel sides.

height (h) = 2, a = 1, b = 3

Applying these values in the formula, we get

= (1/2) x 2 (1 + 3)

= (1/2) x 2 x 4

= 4

ii)

We divide the interval in between 0 to 5 as two parts.

In between 0 to 2, we see the shape trapezium and in between 2 to 5 also we see the trapezium.

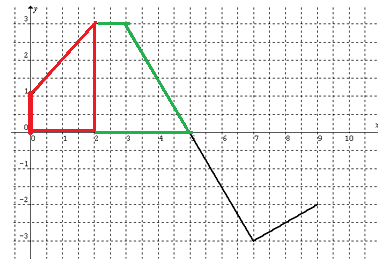
Finding area in between 2 to 5 :

Area of trapezium = (1/2) x h (a + b)

Here a and b are parallel sides.

height (h) = 3, a = 1, b = 3

Applying these values in the formula, we get

= (1/2) x 3 x (1 + 3)

= (1/2) x 3 x 4

= 6

Then,

= 4 + 6

= 10

iii)  

By observing the curve in between 5 and 7, we see the shape triangle and it lies below the x-axis.

Area of triangle = (1/2) x base x height

base = 2, height = 3

= (1/2) x 2 x 3

= 3

Since it lies below the x-axis, the answer should be -3.

iv)  

To find total area, we add 

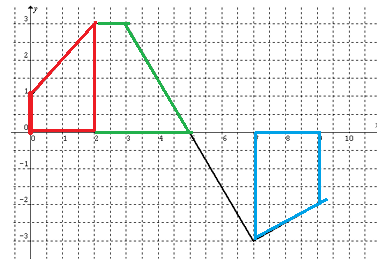
In between 7 to 9, we have trapezium.

height = 2, parallel sides a = 3 and b = 2

Area of trapezium = (1/2) x h x (a + b)

= (1/2) x 2 x (3 + 2)

= 5

Since it lies below the x-axis, the answer should be -5.

Finding the total, we get

= 4 + 6 + (-3) + (-5)

= 10 - 8

= 2

So, the answer is 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.