PROPERTIES OF INEQUALITIES

Addition Property of Inequality

Words : 

Same number can be added to each side of an inequality, and the statement will still be true.

Numbers : 

5 < 12

5 + 3 < 8 + 3

8 < 11

Algebra : 

x < y

x + z < y + z

Subtraction Property of Inequality

Words : 

Same number can be subtracted from each side of an inequality, and the statement will still be true.

Numbers : 

8 < 17

8 - 5 < 17 - 5

3 < 12

Algebra : 

x < y

x - z < y - z

Multiplication Properties of Inequalities

Multiplication by Positive Numbers :

Words : 

Both sides of an inequality can be multiplied by the same positive number, and the statement will still be true.

Numbers : 

5 < 8

5(3) < 8(3)

15 < 24

Algebra : 

If x < y and z > 0, then, 

xz < yz

Multiplication by Negative Numbers :

Words : 

If each side of an inequality is multiplied by the same negative number, you have to reverse the inequality symbol for the statement to still be true.

Numbers : 

8 > 5

8(-3) < 5(-3)

-24 < -15

Algebra : 

If x > y and z < 0, then, 

xz < yz

Division Properties of Inequalities

Division by Positive Numbers :

Words : 

Both sides of an inequality can be multiplied by the same positive number, and the statement will still be true.

Numbers : 

20 < 45

20/5 < 45/5

4 < 9

Algebra : 

If x < y and z > 0, then, 

x/z < y/z

Division by Negative Numbers :

Words : 

If each side of an inequality is divided by the same negative number, you have to reverse the inequality symbol for the statement to still be true.

Numbers : 

45 > 20

45/(-5) < 20/(-5)

-9 < -4

Algebra : 

If x > y and z < 0, then, 

x/z < y/z

What happens when you multiply or divide each side of an inequality by a negative number?

Look at the number line below.

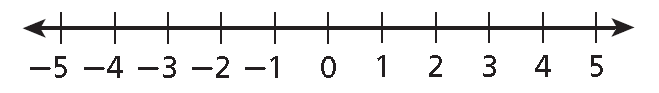
2 < 5 Multiply each side by -1. -2 ? -5 Use the number line to determine the direction of the inequality. -2 > -5

5 > -2 Multiply each side by -1. -5 ? 2 Use the number line to determine the direction of the inequality. -5 < 2

Notice that when you multiply (or divide) both sides of an inequality by a negative number, you must reverse the inequality symbol. This means there is another set of properties of inequality for multiplying or dividing by a negative number.

Note : 

The above explained addition, subtraction, multiplication and division properties are also true for the inequalities that use the symbols >, ≥, and ≤.

Problems on Properties of Inequalities

Find the integers that satisfy each of the following inequalities below.

Example 1 :

16 ≤ 5x + 1 < 31

Solution :

16 ≤ 5x + 1 < 31

Subtracting 1 through out the inequality, we get

16 - 1 ≤ 5x + 1 - 1 < 31 - 1

15 ≤ 5x < 30

Dividing by 5,

15/5 ≤ 5x/5 < 30/5

3 ≤ x < 6

So, the solution is [3, 6).

Example 2 :

0 ≤ (x - 6)/2 < 2

Solution :

0 ≤ (x - 6)/2 < 2

Multiplying by 2 everywhere.

0(2) ≤ (x - 6) < 2(2)

0 ≤ (x - 6) < 4

Adding 6, we get

0 + 6 ≤ x < 4 + 6

6 ≤ x < 10

So, the solution is [6, 10).

Example 3 :

Farmer Taylor is placing a fence around his field. He has 300 meters of fencing but this is not enough.

(a) Form an inequality in terms of x.

(b) Solve the inequality to find the possible width of the

Solution :

a)  Length of the rectangular field = 2x + 5

Width = x meters

Length of fencing he has = 300 m

Perimeter of the rectangular field = 2(length + width)

2(2x + 5 + x) > 300

2(3x + 5) > 300

Dividing by 2, we get 

3x + 5 > 150

Subtracting 5, we get

3x > 150 - 5

3x > 145

x > 145/3

x > 48.3

b)

So, possible width is 48 m.

Example 4 :

The perimeter of the regular pentagon is larger than the perimeter of the equilateral triangle.

(a) Form an inequality in terms of x

(b) Solve the inequality to find the possible range of values

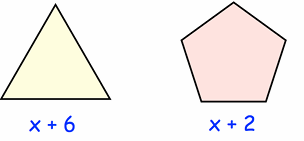
Solution :

Perimeter of equilateral triangle = 3(side length)

Side length = x + 6

= 3(x + 6)

= 3x + 18

Perimeter of pentagon = 5(side length)

= 5(x + 2)

= 5x + 10

a)  Perimeter of regular pentagon > Perimeter of equilateral triangle

5x + 10 > 3x + 18 -----(1)

Subtracting 3x on both sides, 

5x - 3x + 10 > 18

Subtracting 10 on both sides

2x > 18 - 10

2x > 8

Dividing by 2 on both sides

x > 4

b) Applying the value of x which is greater than 4

When x = 5 in (1)

5(5) + 10 > 3(5) + 18

25 + 10 > 15 + 18

35 > 33 (True)

When x = 6 in (1)

5(6) + 10 > 3(6) + 18

30 + 10 > 18 + 18

40 > 36 (True)

When x = 9 in (1)

5(6) + 10 > 3(6) + 18

30 + 10 > 18 + 18

40 > 36 (True)

So, the range will be (4, ∞).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.