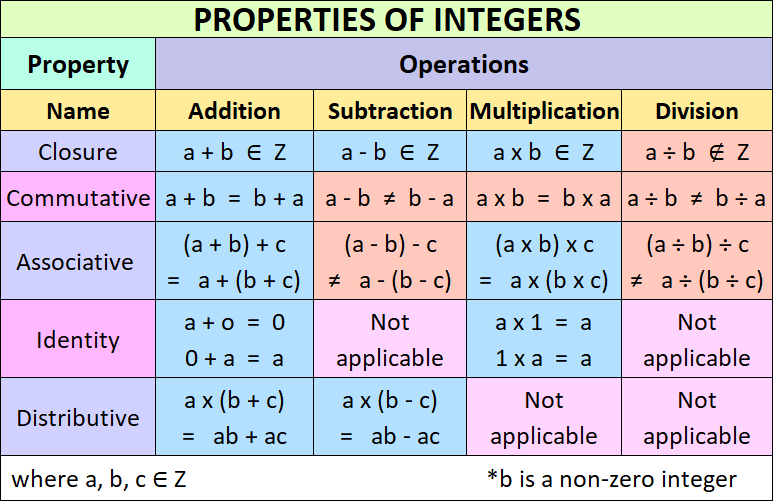
PROPERTIES OF INTEGERS
In Math, the whole numbers and negative numbers together are called integers. The set of all integers is denoted by Z.
Z = {....... - 2, -1, 0, 1, 2,......}, is the set of all integers
Properties of integers determine its operations. These properties help us to solve many equations.
Following are the important properties of integers.
(i) Closure property
(ii) Commutative property
(iii) Associative property
(iv) Identity property
(v) Distributive property
Closure Property of Integers
Addition :
Observe the following examples:
(i) 19 + 23 = 42
(ii) - 10 + 4 = - 6
(iii) 18 + (- 47) = - 29
In general, for any two integers a and b, a + b is an integer.
Therefore the set of integers is closed under addition.
Subtraction :
Observe the following examples:
(i) 12 - 5 = 7
(ii) 5 - 12 = -7
(vi) 18 - (-13) = 18 + 13 = 31
From the above examples, it is clear that subtraction of any two integers is again an integer.
In general, for any two integers a and b, a - b is an integer.
Therefore, the set of integers is closed under subtraction.
Multiplication :
Observe the following:
– 10 × (– 5) = 50
40 × (– 15) = – 600
In general, a × b is an integer, for all integers a and b.
Therefore, integers are closed under multiplication.
Division :
Observe the following examples :
(i) 15 ÷ 5 = 15/5 = 3
(ii) (-3) ÷ 9 = -3/9 = -1/3
(i) 7 ÷ 4 = 7/4 = 1.75
(ii) 1 ÷ 2 = 1/2 = 0.5
From the above examples we observe that integers are not closed under division.
Commutative Property of Integers
Addition :
Two integers can be added in any order. In other words, addition is commutative for integers.
We have 8 + (- 3) = 5 and (- 3) + 8 = 5
So, 8 + (- 3) = (- 3) + 8
In general, for any two integers a and b we can say,
a + b = b + a
Therefore addition of integers is commutative.
Subtraction :
Consider the integers 7 and 4. We see that
7 - 4 = 3
4 - 7 = - 3
Therefore, 7 - 4 ≠ 4 - 7
In general, for any two integers a and b
a - b ≠ b - a
Therefore, we conclude that subtraction is not commutative for integers.
Multiplication :
Observe the following :
5 × (– 6) = – 30 and (– 6) × 5 = – 30
Therefore, 5 × (– 6) = (– 6) × 5
Therefore, multiplication is commutative for integers.
In general, for any two integers a and b, a × b = b × a.
Division :
Observe the following examples :
15 ÷ 5 = 15/5 = 3
5 ÷ 15 = 5/15 = 1/3
Therefore,
15 ÷ 5 ≠ 5 ÷ 15
From the above example, we observe that integers are not commutative under division.
Associative Property of Integers
Addition :
Observe the following example :
Consider the integers 5, – 4 and 7.
Look at
5 + [(– 4) + 7] = 5 + 3 = 8
and
[5 + (– 4)] + 7 = 1 + 7 = 8
Therefore, 5 + [(– 4) + 7] = [5 + (– 4)] + 7
In general, for any integers a, b and c, we can say,
a + (b + c) = (a + b) + c.
Therefore addition of integers is associative.
Subtraction :
Consider the integers 7, 4 and 2
7 - (4 - 2) = 7 - 2 = 5
(7 - 4) - 2 = 3 - 2 = 1
Therefore, 7 - (4 - 2) ≠ (7 - 4) - 2
In general, for any three integers a , b and c
a - (b - c) ≠ (a - b) - c.
Therefore, subtraction of integers is not associative.
Multiplication :
Consider the integers 2, – 5, 6.
Look at
[2 x (-5)] x 6 = -10 x 6 = -60
2 x [(- 5) x 6] = 2 x (-30) = -60
Thus,
[2 x (-5)] x 6 = 2 x [(- 5) x 6]
In general, for any integers a, b, c,
(a × b) × c = a × (b × c)
So, we can say that integers are associative under multiplication.
Division :
Observe the following examples :
12 ÷ (6 ÷ 2) = 12 ÷ 3 = 4
(12 ÷ 6) ÷ 2 = 2 ÷ 2 = 1
Therefore,
12 ÷ (6 ÷ 2) ≠ (12 ÷ 6) ÷ 2
From the above example, we observe that integers are not associative under division.
Identity Property of Integers
Additive Identity :
When we add zero to any integer, we get the same integer.
Observe the example: 5 + 0 = 5.
In general, for any integer a, a + 0 = a.
Therefore, zero is the additive identity for integers.
Multiplicative Identity :
Observe the following:
5 x 1 = 5
1 x (- 7) = -7
This shows that ‘1’ is the multiplicative identity for integers.
In general, for any integer a we have
a x 1 = 1 x a = a
Distributive Property of Integers
Multiplication is Distributive Over Addition :
Consider the integers 12, 9, 7.
Look at
12 x (9 + 7) = 12 x 16 = 192
12 x (9 + 7) = 12 x 9 + 12 x 7 = 108 + 84 = 192
Thus,
12 x (9 + 7) = (12 x 9) + (12 x 7)
In general, for any integers a, b, c.
a x (b + c) = (a x b) + (a x c)
Therefore, multiplication is distributive over addition of integers.
Multiplication is Distributive Over Subtraction :
Consider the integers 12, 9, 7.
Look at
12 x (9 - 7) = 12 x 2 = 24
12 x (9 - 7) = 12 x 9 - 12 x 7 = 108 - 84 = 24
Thus,
12 x (9 - 7) = (12 x 9) - (12 x 7)
In general, for any integers a, b, c.
a x (b - c) = (a x b) - (a x c)
Therefore, multiplication is distributive over subtraction of integers.
Some other Properties of Integers
Zero Division Property :
Division of any non-zero number by zero is meaningless.
Because division by zero is not defined.
Multiplication by Zero :
The product of any nonzero integer with zero is zero.
Observe the following:
5 × 0 = 0
– 8 × 0 = 0
In general, for any nonzero integer a
a × 0 = 0 × a = 0
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
