PROPERTIES OF MATRIX ADDITION

(i)  Matrix addition is commutative :

If A and B are any two matrices of same order, then

A+B = B+A

(ii)  Matrix addition is associative :

If A, B and C are any three matrices of same order, then

A + (B + C)  =  (A + B) + C

(iii)  Existence of additive identity :

Null or zero matrix is the additive identity for matrix addition. If A is a matrix of order m x n, then

A + O  =  O + A  =  A

where O is the null matrix of order m x n.

(iv)  Existence of additive inverse :

For a matrix A, B is called the additive inverse of A if

B + A  =  A + B  =  O

Since

A + (- A)  =  (- A) + A  =  O

-A is the additive inverse of A.

Note :

The additive inverse of a matrix is its negative matrix and it is unique (only one).

Question 1 :

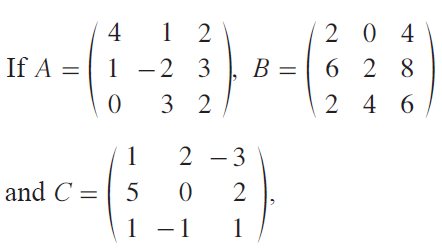
then, verify that A + (B + C) = (A + B) + C.

Solution :

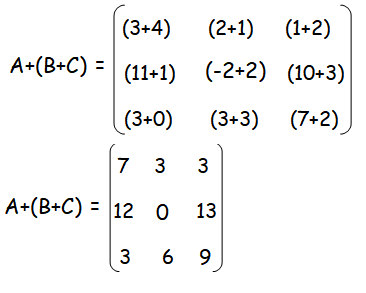
Question 2 :

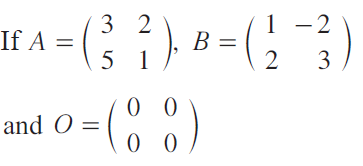
then verify:

(i) A + B = B + A

(ii) A + (- A) = O = (- A) + A

Solution :

(i) 

By finding the sum of matrices A and B, we get the value of A + B.

By finding the sum of matrices B and A, we get the value of B + A.

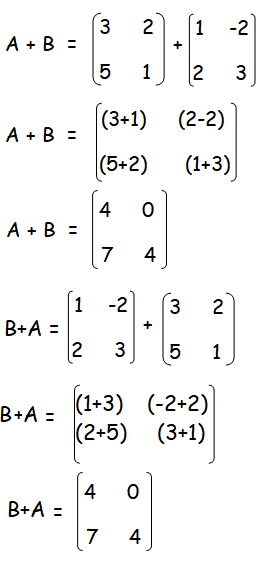
From the above steps, it is clear that

A + B  =  B + A. 

Matrix addition is commutative.

(ii)   By adding A and -A, we get the value of A + (-A).

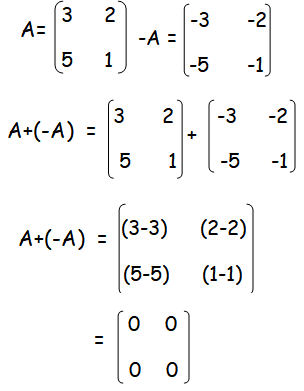
By adding -A and A, we get the value of -A + A.

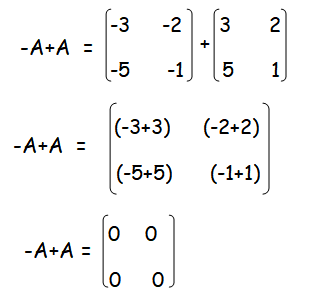
From the above steps, it is clear that 

-A + A  =  0 and A + (-A)  =  0

Question 3 :

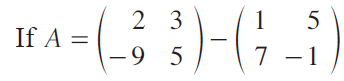
then find the additive inverse of A.

Solution :

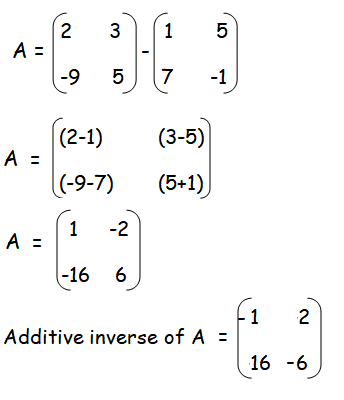
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.