PROPERTIES OF MULTIPLICATION OF INTEGERS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
In Math, the whole numbers and negative numbers together are called integers. The set of all integers is denoted by Z.
Z = {... - 2, - 1,0,1,2, ...}, is the set of all integers
Here, we are going to see the following three properties of multiplication of integers.
(i) Closure property
(ii) Commutative property
(iii) Associative property
(iv) Multiplicative identity
Closure Property of Multiplication of Integers
Observe the following:
– 10 × (– 5) = 50
40 × (– 15) = – 600
In general, a × b is an integer, for all integers a and b.
Therefore, integers are closed under multiplication.
Commutative Property of Multiplication of Integers
Observe the following :
5 × (– 6) = – 30 and (– 6) × 5 = – 30
Therefore,
5 × (– 6) = (– 6) × 5
In general, for any two integers a and b,
a × b = b × a
Therefore, multiplication is commutative for integers.
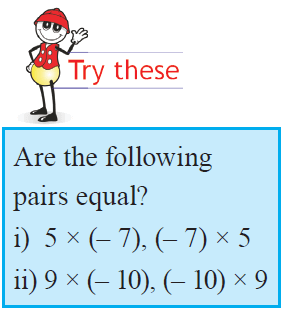
Associative Property of Multiplication of Integers
Consider the integers 2, – 5, 6.
Look at
[2 x (-5)] x 6 = -10 x 6 = -60
2 x [(- 5) x 6] = 2 x (-30) = -60
Thus,
[2 x (-5)] x 6 = 2 x [(- 5) x 6]
In general, for any integers a, b, c,
(a × b) × c = a × (b × c)
So, we can say that integers are associative under multiplication.
Multiplication by Zero
The product of any nonzero integer with zero is zero.
Observe the following:
5 × 0 = 0
– 8 × 0 = 0
In general, for any nonzero integer a
a × 0 = 0 × a = 0

Multiplicative Identity
Observe the following:
5 x 1 = 5
1 x (- 7) = -7
This shows that ‘1’ is the multiplicative identity for integers.
In general, for any integer a we have
a x 1 = 1 x a = a

Distributive Property of Multiplication of Integers
Multiplication is Distributive Over Addition :
Consider the integers 12, 9, 7.
Look at
12 x (9 + 7) = 12 x 16 = 192
12 x (9 + 7) = 12 x 9 + 12 x 7 = 108 + 84 = 192
Thus 12 x (9 + 7) = (12 x 9) + (12 x 7)
In general, for any integers a, b, c.
a x (b + c) = (a x b) + (a x c)
Therefore, multiplication is distributive over addition of integers.
Multiplication is Distributive Over Subtraction :
Consider the integers 12, 9, 7.
Look at
12 x (9 - 7) = 12 x 2 = 24
12 x (9 - 7) = 12 x 9 - 12 x 7 = 108 - 84 = 24
Thus 12 x (9 - 7) = (12 x 9) - (12 x 7)
In general, for any integers a, b, c.
a x (b - c) = (a x b) - (a x c)
Therefore, multiplication is distributive over subtraction of integers.
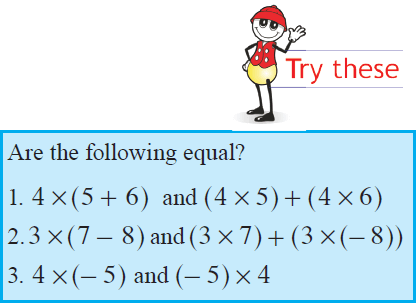
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 18, 26 06:52 PM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
