PROPERTIES OF PERFECT SQUARE

When a number is multiplied by itself, we say that the number is squared.

It is denoted by a number raised to the power 2.

For example, 

3 x 3 = 3² = 9

5 x 5 = 5² = 25

In the example above, 5² is read as 5 to the power of 2 or 5 raised to the power 2 or 5 squared. 25 is the square of 5.

Similarly, 49 and 81 are the squares of 7 and 9 respectively.

The numbers 1, 4, 9, 16, 25, g are called perfect squares or square numbers as 1 = 1², 4 = 2², 9 = 3², 16 = 4²  and so on.

A number is called a perfect square, if it is expressed as the square of a number.

We observe the following properties through the patterns of perfect squares.

Property 1 : 

In perfect squares, the digits at the one’s place are always 0, 1, 4, 5, 6 or 9. The numbers having 2, 3, 7 or 8 at its one' place are not perfect square numbers.

Property 2 :

If a number has 1 or 9 in the one's place then its square ends in 1.

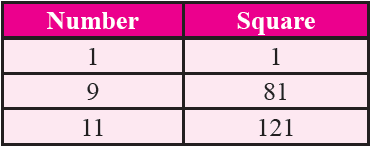
Property 3 :

If a number has 2 or 8 in the one's place then its square ends in 4.

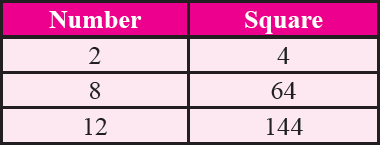
Property 4 :

If a number has 3 or 7 in the one's place then its square ends in 9.

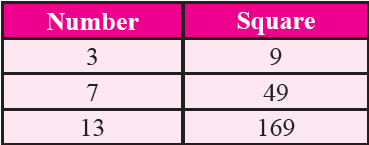
Property 5 :

If a number has 4 or 6 in the one's place then its square ends in 6.

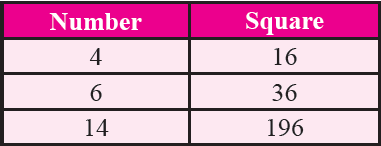
Property 6 :

If a number has 5 in the one's place then its square ends in 5.

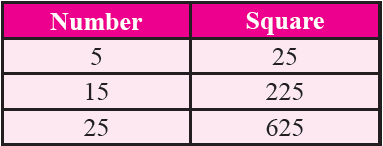
Property 7 :

Consider the following square numbers :

From the perfect squares given above, we infer that

Property 8 :

A perfect square number followed by even number of zeros will be a perfect square and a perfect square number followed by odd number of zeros will not be a perfect square.  

Consider the following square numbers :

Therefore, 100 is a perfect square and 81000 is not a perfect square.

Property 9 :

Square of even numbers is always even. 

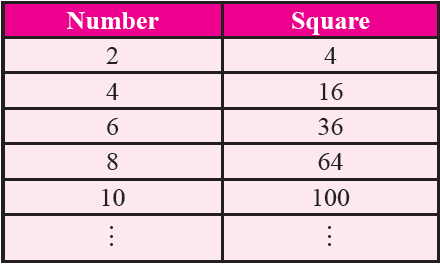
Property 10 :

Square of odd numbers is always odd. 

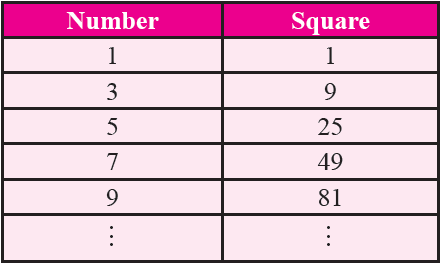
From property 11 and property 12, we infer that

Some Interesting Patterns of Square Numbers

Addition of consecutive odd numbers :

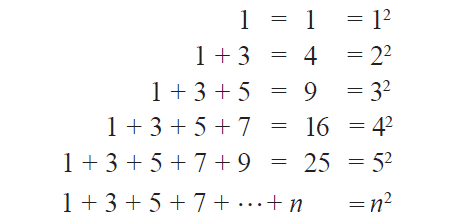
The above figure illustrates the result that the sum of the first n natural odd numbers is n².

And, square of a rational number a/b is given by

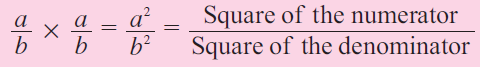
Kaprekar Numbers

Problem 1 :

Which of the following is the square of an odd number?

(a) 256      (b) 361     (c) 144     (d) 400

Solution :

Let us consider the following examples,

1² = 1

2² = 4

3² = 9

4² = 16

Observing these examples,

• square of odd number is odd.
• square of even number is even.

In the given options, option b 361 is the odd number. It must be a square of odd number.

Problem 2 :

Which of the following will have 1 at its units place ?

(a) 19²      (b) 17²     (c) 18²     (d) 16²

Solution :

19² = 19 x 19

Product of unit digit is, 9 x 9 = 81

1 is at the unit place. Then option a is correct.

Problem 3 :

How many natural numbers lie between 18²and 19² ?

(a) 30     (b) 37     (c) 35     (d) 36

Solution :

18²and 19²

18² = 324 and 19² = 361

For example, let us count the numbers in between 1 to 10.

2, 3, 4, 5, 6, 7, 8, 9

There are 8 terms.

= 36 terms

So, in between 18²and 19² we have 36 numbers.

Problem 4 :

Which of the following is not a perfect square?

(a) 361   (b) 1156   (c) 1128    (d) 1681

Solution :

The unit digit of the perfect square will be 

1, 4, 5, 6, 0

8 cannot be the unit digit of the perfect square. So, option c is not a perfect square.

Problem 5 :

A perfect square can never have the following digit at ones place.

(a) 1     (b) 6     (c) 5     (d) 3

Solution :

The unit digit of the perfect square will be 

1, 4, 5, 6, 0

So, 3 will not be unit digit of the perfect square.

Problem 6 :

The value of √(176 + √2401) is 

(a) 14     (b) 15     (c) 16     (d) 17

Solution :

 √(176 + √2401)

√2401 = √7 x 7 x 7 x 7

= 7 x 7

= 49

 √(176 + √2401) = √(176 + 49)

= √225

= √15 x 15

= 15

So, option b is correct.

Problem 7 :

There are __________ perfect squares between 1 and 50.

Solution :

Perfect squares in between 1 and 50 :

1, 4, 9, 16, 25, 36, 49

So, total number of perfect squares is 7.

Problem 8 :

The cube of 100 will have __________ zeroes.

Solution :

100³ = 100 x 100 x 100

= 1000000

= 10⁶

There are 6 zeros.

Problem 9 :

The square of 6.1 is ____________.

Solution :

6.1² = 6.1 x 6.1

= 37.21

Problem 10 :

The square root of a perfect square of n digits will have  n/2 digits if n is even.

Solution :

True

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.