PROPERTIES OF PROPORTION

Following are the properties of proportion :

1. Cross Product Rule

2. Invertendo Property

3. Alternendo Property

4. Componendo Property

5. Dividendo Property

6. Componendo and Dividendo Property

7. Addendo Property

8. Subtrahendo Property

Cross Product Rule

Consider the following proportion :

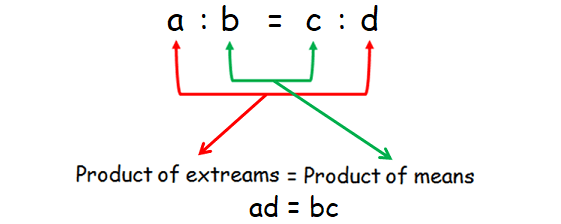
a : b = c : d

a and d ----> extremes

b and c ----> means

In a proportion,

product of extremes = product of means

In the proportion a : b = c : d, we have

ad  =  bc

This property is called cross product rule.

Three quantities a, b, c of the same kind (in same units) are said to be in continuous proportion.

If three quantities a, b, c are in continuous proportion, then the middle term b is called the mean proportional between a and c, a is the first proportional and c is the third proportional.

Since three quantities a, b, c are in continuous proportion, we can write them as

a : b = b : c

Using cross product rule, we can solve for the mean proportion b.

product of means = product of extremes

b² = ac

Taking square root on both sides,

b = √ac

Invertendo Property

Let the two ratios a : b and c : d be in proportion.

a : b = c : d

Then their inverse ratios will also be in proportion, this property is called invertendo property.

b : a = d : c

Alternendo Property

Let the two ratios a : b and c : d be in proportion.

a : b = c : d

By interchanging the means b and c, we get two new ratios:

a : c and b : d

Now, the two ratios a : c and b : c are in proportion.

a : c = b : d

Componendo Property

Let the two ratios a : b and c : d be in proportion.

a : b = c : d

In each ratio, by adding the second term to the first term, we get 

(a + b) : b and (c + d) : d

Now, the two ratios (a + b) : b and (c + d) : d are in proportion.

(a + b) : b = (c + d) : d

Dividendo Property

Let the two ratios a : b and c : d be in proportion.

a : b = c : d

In each ratio, by subtracting the second term from the first term, we get 

(a - b) : b and (c - d) : d

Now, the two ratios (a - b) : b and (c - d) : d are in proportion.

(a - b) : b = (c - d) : d

Componendo and Dividendo

Let the two ratios a : b and c : d be in proportion.

a : b = c : d

In each ratio, add the second term to the first term and take the result as the first term, subtract the second term from the first term and take the result as the second term.

Then, we have

(a + b) : (a - b)

(c + d) : (c - d)

Now, the above two ratios are in proportion.

(a + b) : (a - b) = (c + d) : (c - d)

Addendo Property

Consider the following continued proportion.

a : b = c : d = e : f =..........

Add all the first terms and take the result as the first term and add all the second terms and take the result as the second term.

Then, we get

(a + c + e + ........) : (b + d + f + ........)

Now, the ratio (a + c + e + ........) : (b + d + f + ........) is equal to each ratio in the above continued proportion.

That is,

a : b = c : d = e : f =..... = (a + c + e + .....) : (b + d + f + .....)

Subtrahendo Property

Consider the following continued proportion.

a : b = c : d = e : f =..........

Subtract all the first terms (except the first term in the first ratio 'a') from the first term of the first ratio and  take the result as the first term and subtract all the second terms (except the second term in the first ratio 'b') from the second term of the first ratio and  take the result as the second term.

Then, we get

(a - c - e - ........) : (b - d - f - ........)

Now, the ratio (a - c - e + ........) : (b - d - f - ........) is equal to each ratio in the above continued proportion.

That is,

a : b = c : d = e : f =..... = (a - c - e - .....) : (b - d - f - .....)

Solving Problems Using Properties of Proportion

Problem 1 :

If a : b = c : d = 2.5 : 1.5, what are the values of ad : bc and a + c  :  b + d ?

Solution : 

In the given proportion a : b and c : d, applying cross product rule, we get

ad  =  bc

Dividing by bc on both sides, we get  

ad/bc  =  1

ad/bc  =  1/1

ad : bc  =  1 : 1

Given : a : b  =  c : d  =  2.5 : 1.5 ------ (1)

In the given proportion a : b and c : d, applying the property addendo, we get

a : b  =  c : d  =  (a+b) : (c+d) ------ (2)

From (1) and (2), we get  

(a+b) : (c+d)  =  2.5 : 1.5

(a+b) : (c+d)  =  (2.5x10) : (1.5x10)

(a+b) : (c+d)  =  25 : 15

(a+b) : (c+d)  =  (25/5) : (15/5)

(a+b) : (c+d)  =  5 : 3

Problem 2 :

If a : 3  =  b : 4  =  c : 7, then, find the value of (a+b+c) : c

Solution : 

In the given proportion a : 3  =  b : 4  =  c : 7, applying the property addendo, we get

a : 3  =  b : 4  =  c : 7  =  (a + b + c) : (3 + 4 + 7)

a : 3  =  b : 4  =  c : 7  =  (a + b + c) : 14

Now, all the above four ratios are equal.

Taking the last two ratios, we get

c : 7  =  (a + b + c) : 14

c / 7  =   (a + b + c) / 14

14 / 7  =  (a + b + c) / c

2  =  (a + b + c) / c

or

 (a + b + c) / c  =  2/1

(a + b + c) : c  =  2 : 1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.