PROPERTIES OF QUADRATIC FUNCTIONS

Complete each blank with the most appropriate term or phrase from the given list:

average, completing, down, x-coordinate, minimum, optimization, y-coordinate,  standard, vertex.

Problem 1 :

The highest or lowest point of a parabola is called a

____________.

Solution :

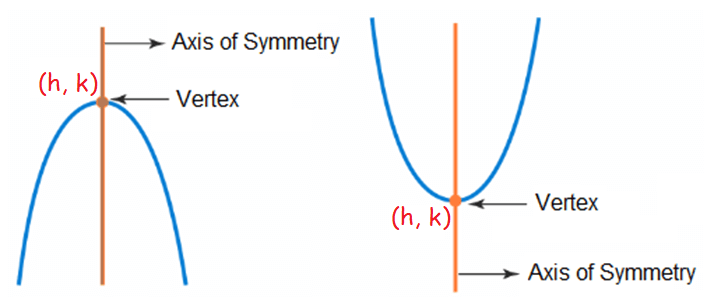
The highest point or lowest point of the parabola is called vertex of the parabola.

Problem 2 :

When 𝑎 is negative, the parabola given by the function f(x) = 𝑎x² + bx + c opens ________

Solution :

When a is negative, the parabola opens downward.

Problem 3 :

When 𝑎 is positive, the parabola given by the function f(x) = 𝑎x² + bx + c has a ________ point.

Solution :

When a is positive, the parabola open up. Then it will have minimum point.

Problem 4 :

When converting the ___________ form of a quadratic function

𝑓(𝑥) = ax² + bx + c

to its vertex form

f(x) = a(x - p)² + q

the process of _____ the square is used.

Solution :

To covert standard form to vertex form, we use the method of completing the square.

Problem 5 :

The extreme value (minimum or maximum) of a quadratic function is the ____________ coordinate of the vertex of its graph.

Solution :

Extreme value will occur in the x-coordinate of the vertex.

Problem 6 :

This extreme value occurs at the _________ coordinate of the vertex.

Solution :

Extreme value will occur at the y-coordinate of the vertex.

Problem 7 :

Application problems that involve finding the minimum or maximum points on a graph of a function are often referred to as _________________ problems.

Solution :

Optimization problems

Problem 8 :

The first coordinate of the vertex of the parabola given by the function 𝑓(𝑥)=𝑎(𝑥 − r₁)(𝑥 − r₂) is the __________ of the roots r₁ and r₂.

Solution :

The x-coordinate of the vertex is the average of x intercepts r₁ and r_2.

Determine the value of the zeros, the equation of the axis of symmetry, the max or min value and the vertex

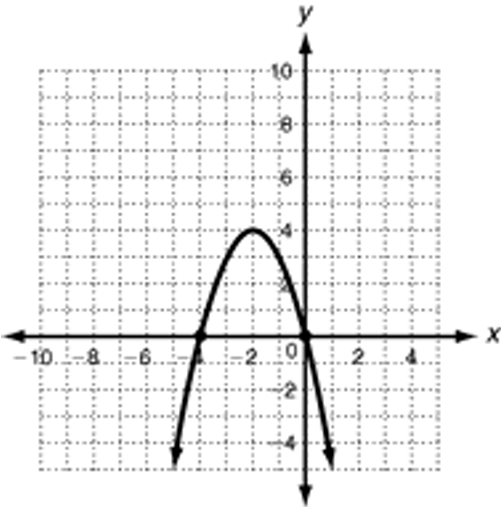
Problem 9 :

Solution :

zeros :

x-intercepts or zeros are -4 and 0.

Axis of symmetry :

x = -2

Max or min value :

Since the parabola opens down, it has maximum value at x = -2

Vertex :

(-2, 4)

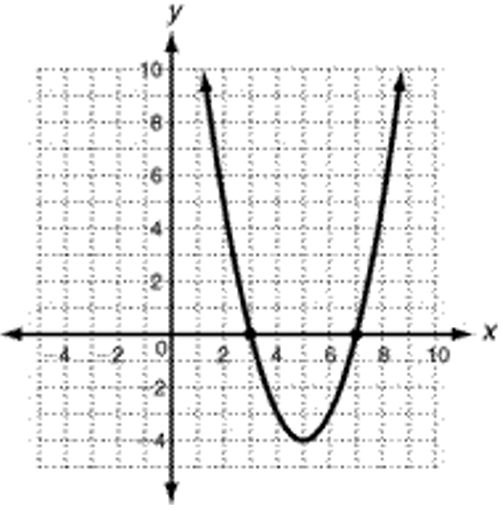
Problem 10 :

Solution :

zeros :

x-intercepts or zeros are 3 and 7.

Axis of symmetry :

x = 5

Max or min value :

Since the parabola opens up, it has minimum value at x = 5

Vertex :

(5, -4)

For each parabola, state its vertex, opening and shape. Then graph it and state the domain and range. 

Problem 11 :

𝑓(𝑥) = 𝑥² − 5𝑥

Solution :

𝑓(𝑥) = 𝑥² − 5𝑥

Comparing the given function with f(x) = a𝑥² + b𝑥 + c, we get 

Direction of opening :

a = 1 > 0, then the parabola opens up.

Converting into vertex form :

𝑓(𝑥) = 𝑥² − 2 ⋅ x ⋅ 5 + 5² - 5²

f(x) = (x - 5)² - 5²

f(x) = (x - 5)² - 25

Vertex is (5, -25)

Domain and Range :

Domain : -∞ ≤ x ≤ ∞

Range : 5 ≤ y ≤ ∞

Problem 12 :

𝑓(𝑥) = 2𝑥² + 12x + 18

Solution :

𝑓(𝑥) = 2𝑥² + 12x + 18

Comparing the given function with f(x) = a𝑥² + b𝑥 + c, we get 

Direction of opening :

a = 2 > 0, then the parabola opens up.

Converting into vertex form :

𝑓(𝑥) = 2𝑥² + 12x + 18

= 2[𝑥² + 6x] + 18

= 2[𝑥² + 2x(3) + 3² - 3²] + 18

= 2[(𝑥 + 3)² - 3²] + 18

= 2(𝑥 + 3)² - 18 + 18

f(x) = 2(𝑥 + 3)²

Vertex is (-3, 0)

Domain and Range :

Domain : -∞ ≤ x ≤ ∞

Range : -3 ≤ y ≤ ∞

For each quadratic function, state its zeros (roots), coordinates of the vertex, opening and shape. Then graph it and identify its extreme (minimum or maximum) value as well as where it occurs.

Problem 12 :

𝑓(𝑥) = (𝑥 − 2)(𝑥 + 2)

Solution :

Roots :

(𝑥 − 2)(𝑥 + 2) = 0

x = 2 and x = -2

Direction of opening :

The parabola opens upward.

x-coordinate of vertex :

x = [2 + (-2)]/2

= 0/2

= 0

y-coordinate:

𝑓(0) = (0 − 2)(0 + 2)

f(0) = -4

Vertex (0, -4)

Problem 12 :

𝑓(𝑥) = -(𝑥 + 3)(𝑥 - 1)

Solution :

Roots :

-(𝑥 + 3)(𝑥 - 1) = 0

x = -3 and x = 1

Direction of opening :

The parabola opens downward.

x-coordinate of vertex :

x = [-3 + 1]/2

= -2/2

= -1

y-coordinate:

𝑓(-1) =-(-1 + 3)(-1 - 1)

f(-1) = -2(-2)

f(-1) = 4

Vertex (-1, 4)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.