PROPERTIES OF QUADRILATERALS

Quadrilateral is a four sided polygon whose sum of internal is 360°.

Following are the different types of quadrilaterals.

(i) Parallelogram

(ii) Rectangle

(iii) Kite

(iv) Rhombus

(v) Square

(vi) Isosceles Trapezoid

Let us look at the properties of a quadrilateral based on its type.

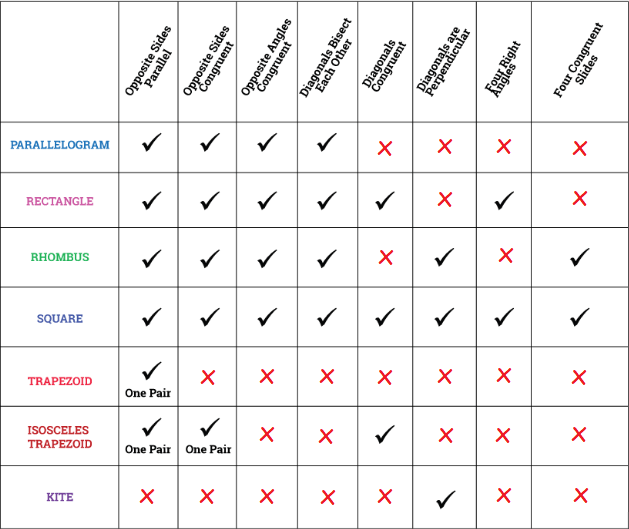
Properties of Parallelogram

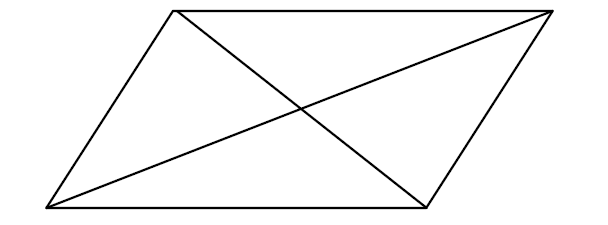
1. Opposite sides are parallel.

2. Opposite sides are congruent.

3. Opposite angles are congruent.

4. Diagonals bisect each other.

5. Any pair of consecutive angles are supplementary.

Properties of Rectangle

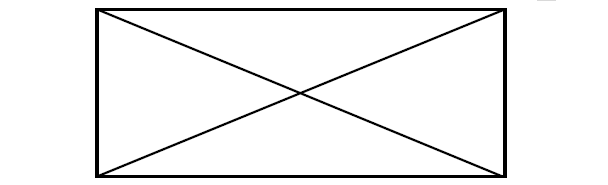
1. All the properties of parallelogram are applicable for rectangle also.

2. All angles are right angles.

3. The diagonals are congruent.

Properties of Kite

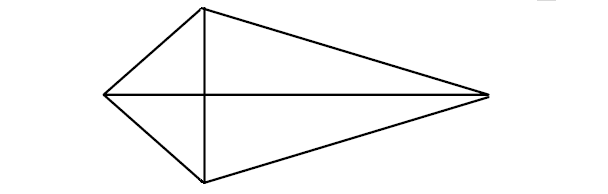
1. Two disjoint pairs of consecutive sides are congruent by definition.

2. The diagonals are perpendicular.

3. One diagonal is the perpendicular bisector of the other.

4. One of the diagonals bisects a pair of opposite angles.

5. One pair of opposite angles are congruent.

Properties of Rhombus

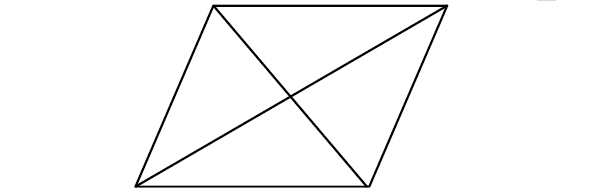
1. All the properties of a parallelogram are applicable for rhombus also.

2. Two consecutive sides are congruent by definition.

3. All sides are congruent.

4. The diagonals bisect the angles.

5. The diagonals are perpendicular bisectors of each other.

6. The diagonals divide the rhombus into four congruent right triangles.

Properties of Square

1. All the properties of a rectangle are applicable for square also.

2. All the properties of a rhombus apply by definition.

3. The diagonals form four isosceles right triangles.

Properties of Isosceles Trapezoid

1. The legs are congruent by definition.

2. The bases are parallel by definition.

3. The lower base angles are congruent.

4. The upper base angles are congruent.

5. The diagonals are congruent.

6. Any lower base angle is supplementary to any upper base angle.

Summary

Solved Questions

Question 1 :

Use the information in the parallelogram shown below to find m∠BAD , m∠ADB , AT, and BD.

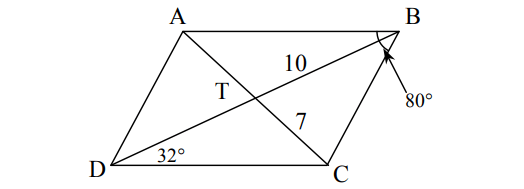
Answer :

In a parallelogram, consecutive angles are supplementary,

m∠BAD + m∠ABC = 180°

Substitute m∠ABC = 80°.

m∠BAD + 80° = 180°

Subtract 80° from both sides.

m∠BAD = 100°

In a parallelogram, opposite angles are congruent,

m∠ADC = m∠ABC

Substitute m∠ABC = 80°.

m∠ADC = 80°

m∠ADB + m∠BDC = 80°

m∠ADB + 32° = 80°

Subtract 32° from both sides.

m∠ADB = 48°

In a parallelogram, diagonals bisect each other :

AT = 7

BD = 10

Question 2 :

Use the information in the rhombus shown below to find m∠SPQ , m∠STR , RQ and RT.

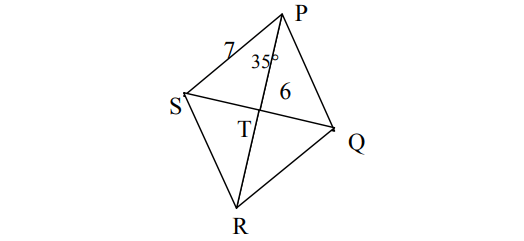
Answer :

In a rhombus, diagonals bisect opposite angles,

m∠SPQ = 70°

In a rhombus, diagonals are perpendicular,

m∠STR = 90°

In a rhombus, all sides are congruent,

RQ = 7

In a rhombus, diagonals bisect each other,

RT = 6

Question 3 :

Given that Q and R are midpoints in the trapezoid shown below to find m∠QMN, m∠QRN and QR.

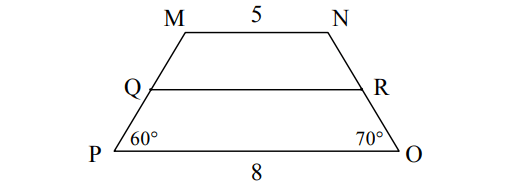
Answer :

Since MN is parallel to PO, ∠OPM and m∠PMN are supplementary.

m∠OPM + m∠PMN = 180°

m∠OPM + m∠QMN = 180°

Substitute m∠OPM = 60°.

60° + m∠QMN = 180°

Subtract 60° from both sides.

m∠QMN = 120°

Since Q and R are midpoints, then QR is parallel to the bases and with parallel lines, corresponding angles are congruent.

m∠QRN = 70°

Length of QR :

QR = (1/2)(5 + 8)

= (1/2)(13)

= 6.5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.