PROPERTIES OF RADICALS
1. If two or more radicals are multiplied with the same index, you can take the radical once and multiply the numbers inside the radicals.
n√a x n√b = n√(a x b)
2. If two radicals are in division with the same index, you can take the radical once and divide the numbers inside the radicals.
n√a/n√b = n√(a/b)
3. One number can be taken out of a square root for every two same numbers multiplied inside the square root. And also, one number can be taken out of a cube root for every three same numbers multiplied inside the cube root and so on.
√4 = √(2 x 2) = 2
3√8 = 3√(2 x 2 x 2) = 2
4. A radical with index n can be written as exponent 1/n.
n√a = a1/n
√a = a1/2
3√a = a1/3
5. Addition and subtraction of two or more radicals can be performed with like radicals and like radicands only.
Like radicals - Radicals with the same index
Radicand - The number inside the radical
For example, 9√3 and 4√3 can be added or subtracted. Because the numbers inside the square roots are same.
9√3 + 4√3 = 13√3
9√3 - 4√3 = 5√3
6. If a radical with index n is moved from one side of the equation to the other side, it will become the exponent n.
n√x = a
x = an
7. If an exponent n is moved from one side of the equation to the other side, it will become a radical with index n.
yn = b
y = n√b
8. If the digit in one's place of a number is 2, 3, 7 or 8, then the number can not be a perfect square. So the square root of such numbers will be irrational.
For example, √23 = 4.795831.........
9. If a number ends with odd number of zeros, then, the square root of the number will be irrational.
For example, √3000 = 54.772255.......
10. The square root of a perfect square is always a rational number.
√4 = √(2 x 2) = 2
√25 = √(5 x 5) = 5
11. The square root of an even perfect square number is always even and the square root of an odd perfect square number is always is odd.
For example,
√64 = 8
√81 = 9
12. Square root of a negative number is considered to be an imaginary value.
For example, √(-2), √(-9).
Solved Problems
Problem 1 :
Simplify :
√6 ⋅ √15
Solution :
= √6 ⋅ √15
= √(6 ⋅ 15)
= √(2 ⋅ 3 ⋅ 3 ⋅ 5)
= 3√(2 ⋅ 5)
= 3√10
Problem 2 :
Simplify :
√35 ÷ √7
Solution :
= √35 ÷ √7
= √(35/7)
= √5
Problem 3 :
Simplify :
3√425 + 4√68
Solution :
Decompose 425 and 68 into prime factors using synthetic division.
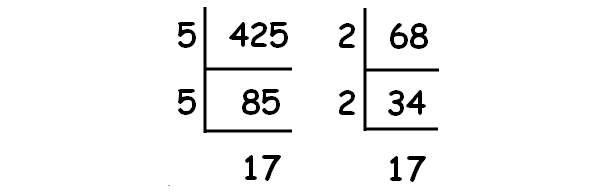
|
√425 = √(5 ⋅ 5 ⋅ 17) √425 = 5√17 |
√68 = √(2 ⋅ 2 ⋅ 17) √68 = 2√17 |
3√425 + 4√68 :
= 3(5√17) + 4(2√17)
= 15√17 + 8√17
= 23√17
Problem 4 :
Simplify :
√243 - 5√12 + √27
Solution :
Decompose 243, 12 and 27 into prime factors using synthetic division.
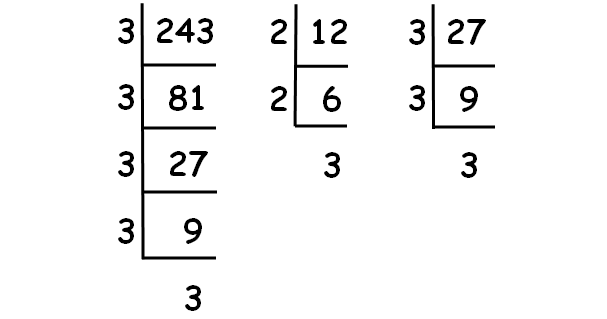
√243 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) = 9√3
√12 = √(2 ⋅ 2 ⋅ 3) = 2√3
√27 = √(3 ⋅ 3 ⋅ 3) = 3√3
√243 - 5√12 + √27 :
= 9√3 - 5(2√3) + 3√3
= 9√3 - 10√3 + 3√3
= 2√3
Problem 5 :
Simplify :
√4 + 3√27 + 4√64
Solution :
√4 = √(2 ⋅ 2) = 2
3√27 = 3√(3 ⋅ 3 ⋅ 3) = 3
4√625 = 4√(5 ⋅ 5 ⋅ 5 ⋅ 5) = 5
√4 + 3√27 + + 4√64 :
= 2 + 3 + 5
= 10
Problem 6 :
Simplify :
3√4 ⋅ 3√16
Solution :
= 3√4 ⋅ 3√16
= 3√(4 ⋅ 16)
= 3√(4 ⋅ 4 ⋅ 4)
= 4
Problem 7 :
If 3√a = 1/2, then find the value of a.
Solution :
3√a = 1/2
a = (1/2)3
a = 13/23
a = 1/8
Problem 8 :
If (3√8)7 ⋅ (√2)-4 = 2k, then solve for k.
Solution :
(3√8)7 ⋅ (√2)-4 = 2k
27 ⋅ (21/2)-4 = 2k
27 ⋅ 2-2 = 2k
27 - 2 = 2k
25 = 2k
k = 5
Problem 9 :
The ratio of the length to the width of a golden rectangle is (1+√5) : 2. The dimensions of the face of the Parthenon in Greece form a golden rectangle. What is the height h of the Parthenon?

Solution :
(1 + √5) : 2 = 31 : h
(1 + √5) / 2 = 31 / h
Doing cross multiplication, we get
h = 2(31) / (1 + √5)
h = 62/(1 + √5)
Rationalizing the denominator, we get
h = [62/(1 + √5)] [(1 - √5)/(1 - √5)]
= 62(1 - √5) / (12 - √52)
= 62(1 - √5) / (1 - 5)
= 62(1 - √5) / (-4)
= -15.5(1 - 2.23)
= -15.5 + 34.56
= 19.06
So, the height is about 19 meters.
Problem 10 :
A sports teacher wants to arrange 6000 students in a field such that the number of rows is equal to number of columns. Find the number of rows if 71 were left out after arrangement.
Solution :
Total number of students = 6000
Number of students left = 6000 - 71
= 5929
Since the number of rows and number of columns should be filled with the same number of students, we have to find the square root of 5929.
√5929 = √(7 x 7 x 11 x 11)
= 7 x 11
= 77
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18) -
Derivative of Absolute Value of x Using Limit Definition
Apr 23, 25 11:11 AM
Derivative of Absolute Value of x Using Limit Definition
