PROPERTIES OF SQUARE NUMBERS

When a number is multiplied by itself, the resulting number is called as a square number. 

For example, when we multiply 5 by 5, we get 5² = 25. Here, 25 is a square number.

In geometry, the area of a square is the finest example of a square number. Area of a square = Side × Side = Side², because all the sides of a square are equal. This means the area of a square is always a square number.

Square numbers are always positive and they can never be negative because when a negative number is multiplied by the same negative number, it results in a positive number.

For example, (-7)² = -7 x -7 = 49 (two negative signs multiplied by each other result in a positive sign). When we multiply -7 by -7, the result is 49 and it is a positive square number. Here are some examples of square numbers.

2 x 2 = 4

-8 x -8 = 64

15 x 15 = 225

We observe the following properties through the patterns of square numbers.

Property 1 : 

In square numbers, the digits at the unit’s place are always 0, 1, 4, 5, 6 or 9. The numbers having 2, 3, 7 or 8 at its units' place are not perfect square numbers.

Property 2 :

If a number has 1 or 9 in the unit's place then its square ends in 1.

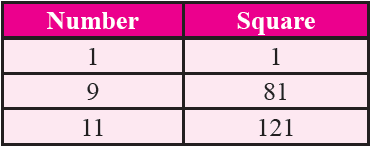
Property 3 :

If a number has 2 or 8 in the unit's place then its square ends in 4.

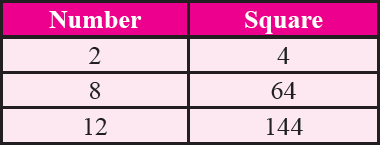
Property 4 :

If a number has 3 or 7 in the unit's place then its square ends in 9.

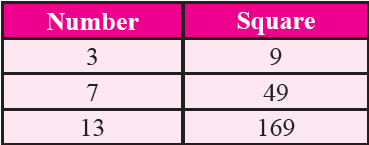
Property 5 :

If a number has 4 or 6 in the unit's place then its square ends in 6.

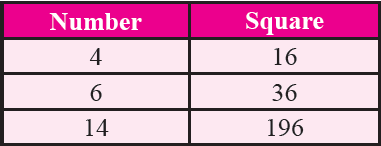
Property 6 :

If a number has 5 in the unit's place then its square ends in 5.

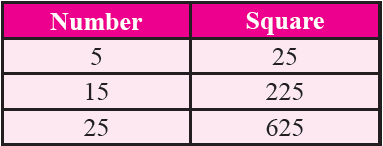
Property 7 :

Consider the following square numbers :

From the square numbers given above, we infer that

Property 8 :

Consider the following square numbers :

Therefore, 100 is a perfect square and 81000 is not a perfect square.

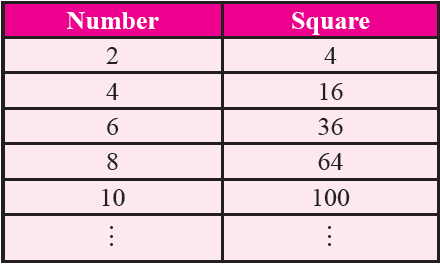
Property 9 :

Square of even numbers is always even. 

It has been illustrated in the table given below.

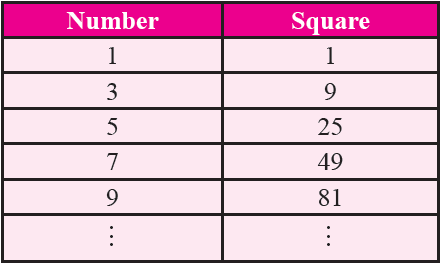
Property 10 :

Square of odd numbers is always odd. 

It has been illustrated in the table given below.

From properties 9 and 10, we infer that

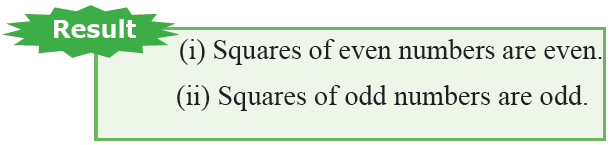
Some Interesting Patterns of Square Numbers

Addition of consecutive odd numbers :

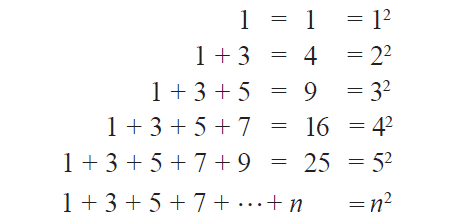
The above figure illustrates the result that the sum of the first n natural odd numbers is n².

And, square of a rational number a/b is given by

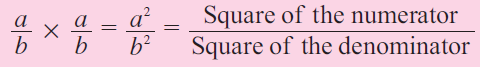
Kaprekar Numbers

Problem 1 :

Observe the following pattern and fill in the blanks.

1 + 3 = 2²

1 + 3 + 5 = 3²

1 + 3 + 5 + 7 = ___________

1 + 3 + 5 + 7 + 9 = ___________

1 + 3 + 5 + 7 + 9 + 11 = ___________

1 + 3 + 5 + 7 + 9 + 11 + 13 = ___________

Solution :

By observing the series,

1 + 3 = 2²

1 + 3 + 5 = 3²

We know that sum of two consecutive odd numbers will be the square of that many numbers. For example, if we add 3 consecutive odd numbers, then we get the answer as 3².

In this way,

1 + 3 + 5 + 7 = 4²

1 + 3 + 5 + 7 + 9 = 5²

1 + 3 + 5 + 7 + 9 + 11 = 6²

1 + 3 + 5 + 7 + 9 + 11 + 13 = 7²

Problem 2 :

Which of the following numbers are perfect squares?

11, 16, 32, 36, 50, 64, 75

Solution :

Checking 11 is perfect square or not :

Since the unit digit is 1, we may use the options

1 x 1 = 1

9 x 9 = 81

No options is given the square of some number as 1, then 11 is not a perfect square.

Checking 16 is perfect square or not :

16 = 4 x 4 ==> 4²

So, 16 is a perfect square.

Checking 32 is perfect square or not :

Since 2 is at the unit place and multiplying any two same numbers we will not get 2. So, 32 is not a perfect square.

Checking 36 is perfect square or not :

36 = 6 x 6 ==> 6²

So, 36 is a perfect square.

Checking 50 is perfect square or not :

Since we have one zero, it cannot written as product of two same numbers. Then 50 is not a perfect square.

Checking 64 is perfect square or not :

64 = 8 x 8 ==> 8²

Then 64 is a perfect square.

Checking 75 is perfect square or not :

Since we have 5 at the unit place, we try

5 x 5 ==> 25

15 x 15 ==> 225

So, 75 is not a perfect square.

Problem 3 :

Which of the following numbers are perfect squares of even numbers?

121, 225, 784, 841, 576, 6561

Solution :

The odd numbers are 121, 225, 841, 6561

Square of odd number must be odd. But square of even number must be even. Then 784, 576 are perfect squares which are even.

Problem 4 :

Which of the following numbers are perfect squares?

100, 205000, 3610000, 212300000

Solution :

100 and 3610000 are consisting even number of zeroes. Then these are perfect squares.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.