PROPERTIES OF STANDARD DEVIATION

The best measure of dispersion is, usually, standard- deviation which does not possess the demerits of range and mean deviation.

SD for a given set of observations is defined as the root mean square deviation when the deviations are taken from the AM of the observations.

Let the  variable "x" assume "n" values  as given below

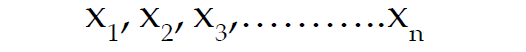
Then, the formula for SD is given by

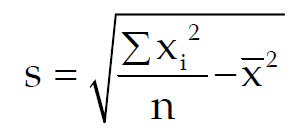
For a grouped frequency distribution, the SD is given by

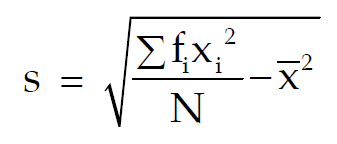
Properties of Standard Deviation

1)  If all the observations assumed by a variable are constant i.e. equal, then the SD is zero. This means that if all the values taken by a variable x is k, say , then s = 0. This result applies to range as well as mean deviation.

2)  SD remains unaffected due to a change of origin but is affected in the same ratio due to a change of scale i.e., if there are two variables x and y related as y = a+bx for any two constants a and b, then SD of y is given by

SD of 'y'  =  |b| x SD of 'x'

3)  If there are two groups containing n₁ and n₂ observations, x̄₁ and x̄₂ as respective arithmetic means, S₁ and S₂ as respective standard deviations, then combined SD is given by 

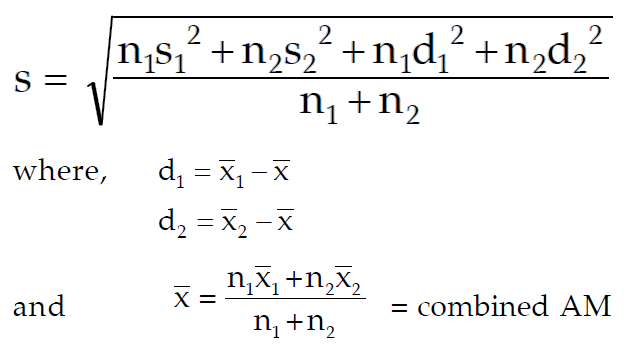
Question 1 :

The standard deviation of 20 observations is √5. If each observation is multiplied by 2, find the standard deviation and variance of the resulting observations.

Solution :

Here √5 is the standard deviation of 20 observations. Now we need to find the standard deviation and variance if each observation is multiplied by 2.

Standard deviation (σ)  =  2√5

Question 2 :

Calculate the standard deviation of the first 13 natural numbers.

Solution :

=  √(n² -1)/12

=  √(13² -1)/12

=  √(169 -1)/12

=  √168/12

=  √14

=  3.7416

=  3.74

So, standard deviation for first 13 numbers is 3.74.

Question 3 :

Calculate the standard deviation of the following data      

10, 20, 15, 8, 3, 4

Solution :

First, we have to write the given data in the ascending order.

3, 4, 8, 10, 15, 20

Since the given numbers are small we can use direct method to find standard deviation.

Σx  =  60, Σx² = 814

σ  =  √(Σx²/n) - (Σ x/n)²

=  √(814/6) - (60/6)²

=  √(135.67 - 10²)

=  √(135.67-100)

=  √35.67

=  5.97

So, the standard deviation is 5.97.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.