PROPERTIES OF TANGENTS TO A CIRCLE

Property 1 :

A tangent line intersects a circle at exactly one point, called the point of tangency. 

Property 2 :

A line is tangent to a circle if and only if it is perpendicular to a radius drawn to the point of tangency. 

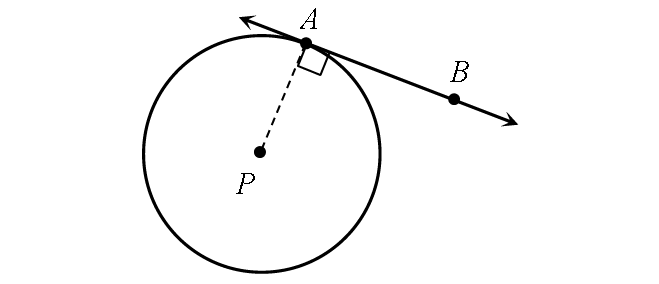
Property 3 :

If two segments from the same external point are tangent to a circle, then they are congruent. 

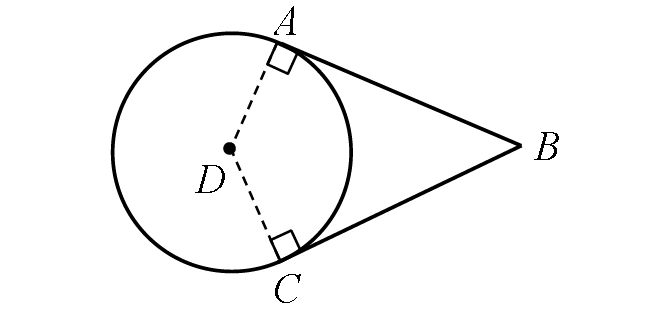
In the diagram shown above,

BA  ≅  BC 

If two segments from the same external point are tangent to a circle, then they are congruent. 

Property 4 :

If a polygon is inscribed around a circle, the all sides of the polygon are tangent to the circle. 

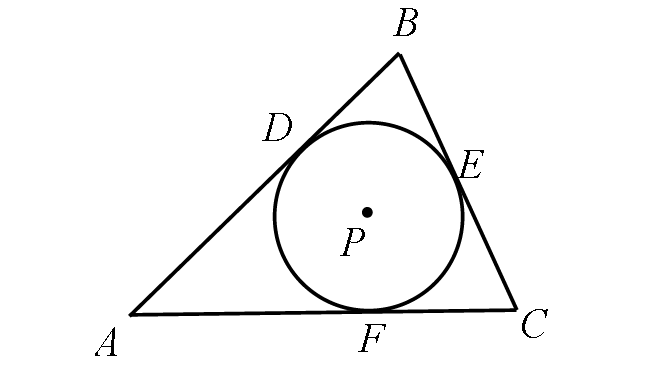
Solved Examples

Example 1 : 

Determine if the line segment AB is tangent to circle P.  

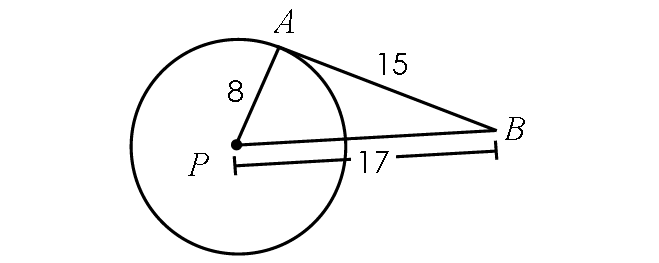
Solution : 

If the line segment AB is tangent to circle P, it is perpendicular to the radius PA.

Then, m∠PAB = 90° and triangle PAB has to be a right triangle. 

Using Pythagorean Theorem, verify whether triangle PAB is a right triangle.  

PA² + PB²  =  PB²

8² + 15²  =  17²  ?

64 + 225  =  289  ?

289  =  289  ?

The above result is true.

So, triangle PAB is a right triangle and m∠PAB = 90°.

Hence, the line segment AB is tangent to circle P.  

Example 2 : 

Determine if the line segment YX is tangent to circle Z.  

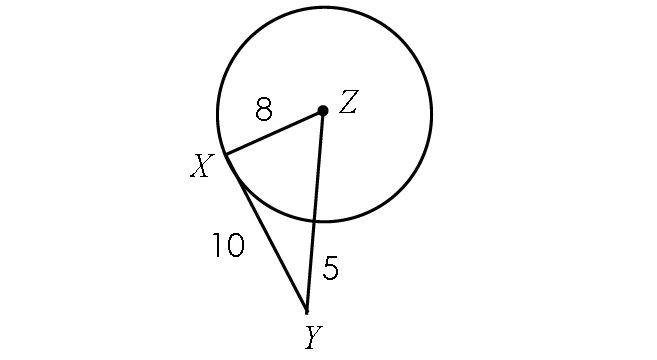
Solution : 

Find the length of ZY : 

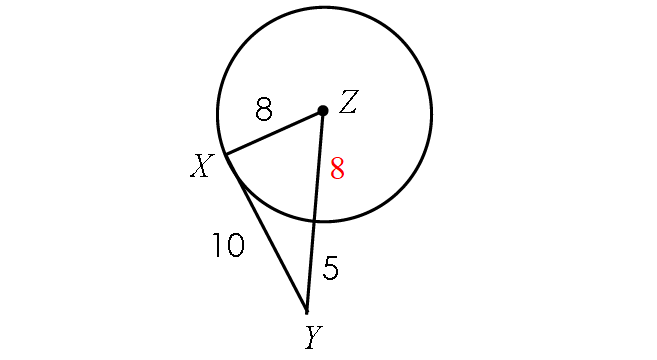
ZY  =  Radius + 5

ZY  =  8 + 5

ZY  =  13

If the line segment YX is tangent to circle Z, it is perpendicular to the radius ZX.

Then, m∠ZXY = 90° and triangle ZXY has to be a right triangle. 

Using Pythagorean Theorem, verify whether triangle ZXY is a right triangle.  

ZX² + XY²  =  ZY²

8² + 10²  =  13²  ?

64 + 100  =  169  ?

164  =  169  ?

The above result is false.

So, triangle ZXY is not a right triangle and m∠ZXY ≠ 90°.

Hence, the line segment YX is not tangent to circle Z.  

Example 3 : 

If the line segment JK is tangent to circle L, find x.   

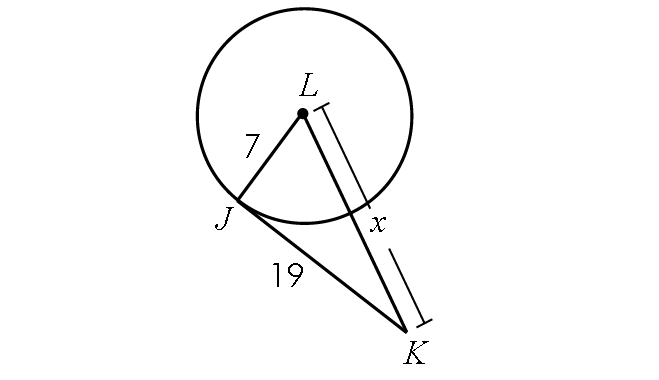
Solution : 

Because JK is tangent to circle L, m∠LJK = 90° and triangle LJK is a right triangle. 

BY Pythagorean Theorem, 

LJ² + JK²  =  LK²

7² + 19²  =  x²

49 + 361  =  x²

49 + 361  =  x²

400  =  x²

Take square root on both sides. 

20  =  x

Example 4 :

Find x.   

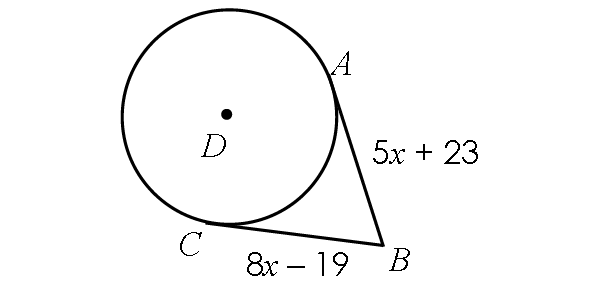
Solution : 

Two segments BC and BA are tangent to circle D from from the same external point B. 

So, they are equal in length. 

BC  =  BA

8x - 19  =  5x + 23  

Subtract 5x from each side. 

3x - 19  =  23

Add 19 to each side. 

3x  =  42

Divide each side by 3. 

x  =  14

Example 5 :

Find x.   

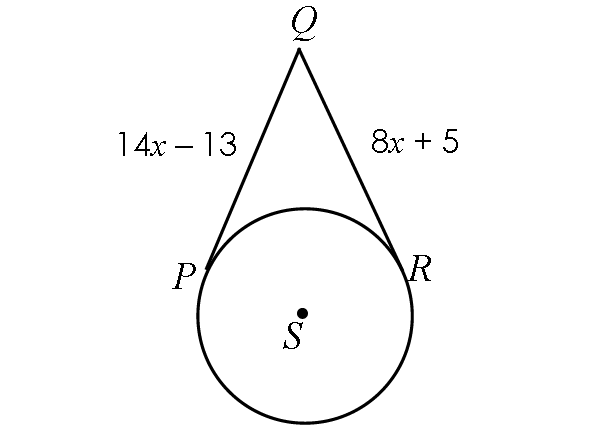
Solution : 

Two segments QP and QR are tangent to circle S from from the same external point Q. 

So, they are equal in length. 

QP  =  QR

14x - 13  =  8x + 5

Subtract 8x from each side. 

6x - 13  =  5

Add 13 to each side. 

6x  =  18

Divide each side by 6. 

x  =  3

Example 6 :

Find SV.   

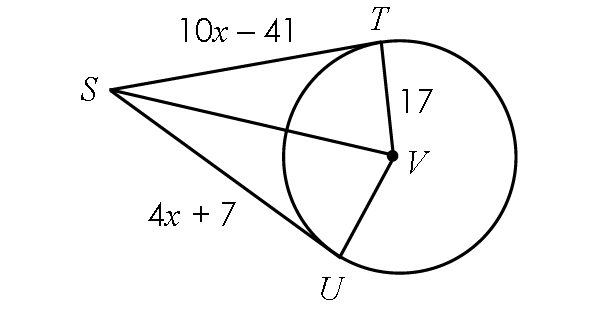
Solution : 

Two segments ST and SU are tangent to circle V from from the same external point V. 

So, they are equal in length. 

ST  =  SU

10x - 41  =  4x + 7

Subtract 4x from each side. 

6x - 41  =  7

Add 41 to each side. 

6x  =  48

Divide each side by 6. 

x  =  8

Find the length of ST : 

ST  =  10(8) - 41

ST  =  80 - 41

ST  =  39

Because ST is tangent to circle V, m∠STV = 90° and triangle STV is a right triangle. 

BY Pythagorean Theorem, 

SV²  =  ST² + TV²

SV²  =  39² + 17²

SV²  =  1521 + 289

SV²  =  1810

Take Square root on both sides. 

SV  ≈  42.5

Example 7 :

Find the perimeter of ΔDEF.

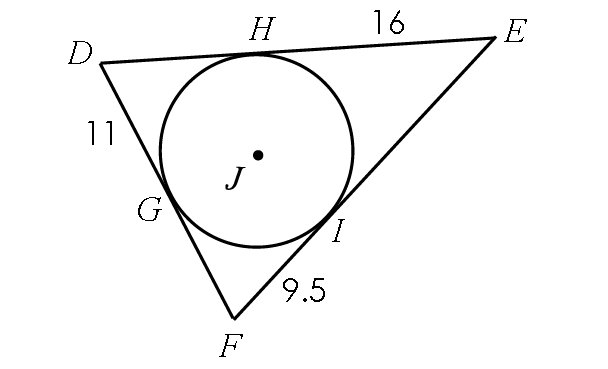
Solution : 

Using properties, we can find the missing lengths. 

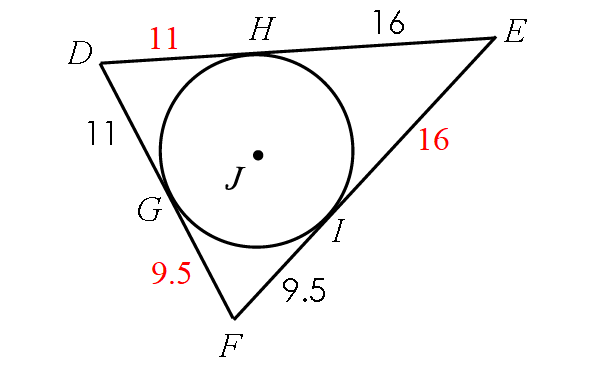
Perimeter of ΔDEF : 

=  DE + EF + FD

=  (11 + 16) + (16 + 9.5) + (9.5 + 11)

=  27 + 25.5 + 20.5

=  73 units

Example 8 :

Find the perimeter of quadrilateral PQRS. 

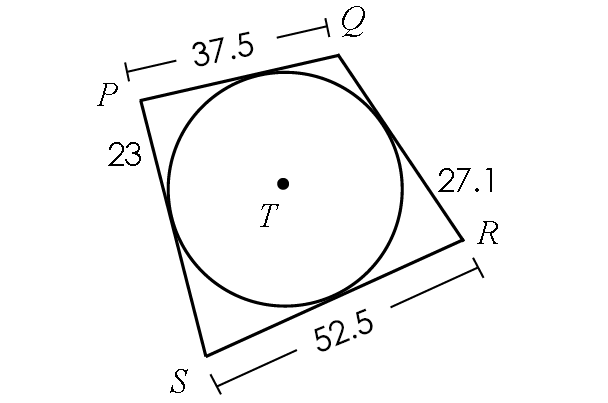
Solution : 

Using properties, we can find the missing lengths. 

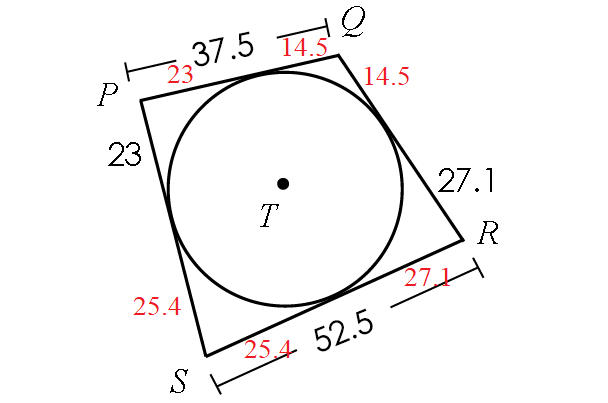
Perimeter of the quadrilateral PQRS : 

=  PQ + QR + RS + SP

=  37.5 + (14.5 + 27.1) + 52.5 + (25.4 + 23)

=  37.5 + 41.6 + 52.5 + 48.4

=  180 units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.