PROPORTION
An equality of two ratios is called a proportion.
Four quantities a, b, c, d are said to be in proportion, if
a : b = c : d (also written as a : b :: c : d)
That is,
a/b = c/d
The quantities a, b, c, d are called terms of the proportion; a, b, c and d are called its first, second, third and fourth terms respectively.
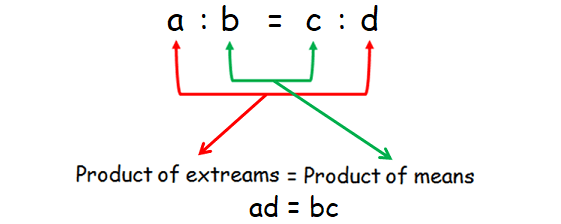
First and fourth terms are called extremes (or extreme terms) and second and third terms are called means (or middle terms).
In a proportion,
product of extremes = product of means
If a : b = c : d are in proportion, then,
ad = bc
This is called cross product rule.
Three quantities a, b, c of the same kind (in same units) are said to be in continuous proportion.
If three quantities a, b, c are in continuous proportion, then the middle term b is called the mean proportional between a and c, a is the first proportional and c is the third proportional.
Since three quantities a, b, c are in continuous proportion, we can write them as
a : b = b : c
Using cross product rule, we can solve for the mean proportion b.
product of means = product of extremes
b2 = ac
Taking square root on both sides,
b = √ac
Solving Problems Using Proportion
Problem 1 :
If x, 2, 10 and 5 are in proportion, find the value of x.
Solution :
x : 2 = 10 : 5
Using cross product rule,
x ⋅ 5 = 2 ⋅ 10
5x = 20
Divide both sides by 5.
x = 4
Problem 2 :
Find the fourth proportional to 4, 5, 12.
Solution :
Let x be the fourth proportional.
4 : 5 = 12 : x
Using cross product rule,
4 ⋅ x = 5 ⋅ 12
4x = 60
Divide both sides by 4.
x = 15
So, the fourth proportion is 15.
Problem 3 :
Find the third proportion to 2.4, 9.6.
Solution :
Let x be the third proportional.
2.4 : 9.6 = 9.6 : x
Using cross product rule,
2.4 ⋅ x = 9.6 ⋅ 9.6
2.4x = 92.16
Divide both sides by 2.4.
x = 38.4
So, the third proportion is 38.4.
Problem 4 :
Find the mean proportion between 1.25 and 1.8.
Solution :
Let x be the mean proportion between 1.25 and 1.8.
1.25 : x = x : 1.8
x2 = 1.25 ⋅ 1.8
x2 = 2.25
Taking square root on both sides,
x = 1.5
Problem 5 :
If the cost of 7 units of a product is $63, find the cost of 9 units of the same product.
Solution :
Let x be the cost of 9 units.
cost of 7 units ----> $63
cost of 9 units ----> $x
We can form a proportion with the four quantities 7, 9, 63 and x.
7 : 9 = = 63 : x
Using cross product rule,
7 ⋅ x = 9 ⋅ 63
7x = 567
Divide both sides by 7.
x = 81
So, the cost of 9 units is $81.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 103)
Jan 25, 25 01:00 AM
Digital SAT Math Problems and Solutions (Part - 103) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Jan 25, 25 12:52 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 102)
Jan 24, 25 12:30 PM
Digital SAT Math Problems and Solutions (Part - 102)