PROPORTIONAL AND NONPROPORTIONAL SITUATIONS USING A TABLE
About "Proportional and nonproportional situations using a table"
Proportional and nonproportional situations using a table :
If there is not a constant rate of change in the data displayed in a table, then the table represents a nonlinear nonproportional relationship.
A linear relationship represented by a table is a proportional relationship when the quotient of each pair of numbers is constant. Otherwise, the linear relationship is nonproportional.
Proportional and nonproportional situations using a table - Examples
Example 1 :
Determine if the linear relationship represented by the table given below is a proportional or nonproportional relationship.
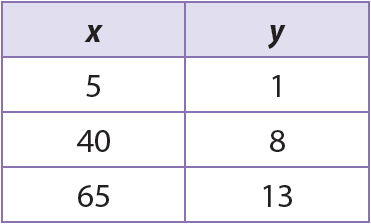
Solution :
From the table, find the ratio between each value of "y" and its corresponding value of "x".
y/x = 1/5 = 1/5
y/x = 8/40 = 1/5
y/x = 13/65 = 1/5
Hence, the ratio between the values of "y" and and their corresponding values of "x" is constant. Hence, the relationship represented by the table given above is proportional.
Example 2 :
Determine if the linear relationship represented by the table given below is a proportional or nonproportional relationship.
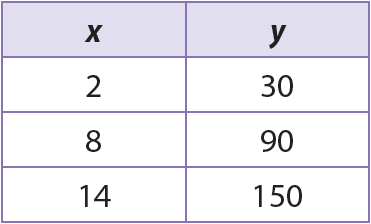
Solution :
From the table, find the ratio between each value of "y" and its corresponding value of "x".
y/x = 30/2 = 15
y/x = 90/8 = 11.25
y/x = 150/14 = 10.71
Hence, the ratio between the values of "y" and and their corresponding values of "x" is not constant. Hence, the relationship represented by the table given above is nonproportional.
Example 3 :
The values in the table represent the numbers of U.S. dollars three tourists traded for Mexican pesos. The relationship is linear. Is the relationship proportional or nonproportional ?
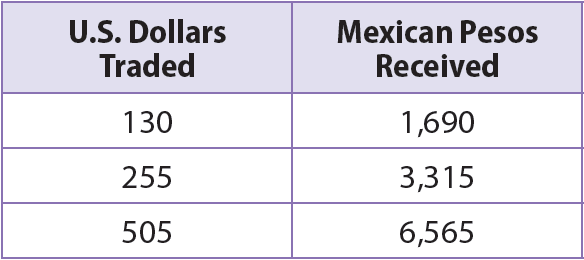
Solution :
From the table, find the ratio between each value of "Mexican pesos received" and its corresponding value of "U.S. dollars traded".
Let "M" stand for Mexican pesos received and "U" stand for U.S. dollars traded
U/M = 1,690/130 = 13
U/M = 3,315/255 = 13
U/M = 6,565/505 = 13
Hence, the ratio of pesos received to dollars traded is constant at 13 Mexican pesos per U.S. dollar. This is a proportional relationship.
After having gone through the stuff given above, we hope that the students would have understood, how to use tables to identify proportional and nonproportional situations.
Apart from the stuff given above, if you want to know more about "Proportional and nonproportional situations using a table", please click here
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
WORD PROBLEMS
HCF and LCM word problems
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
