PROPORTIONAL AND NONPROPORTIONAL SITUATIONS

Example 1 :

The graph shows the relationship between the weight of an object on the Moon and its weight on Earth. Explain why this relationship is proportional and also write an equation for the relationship.

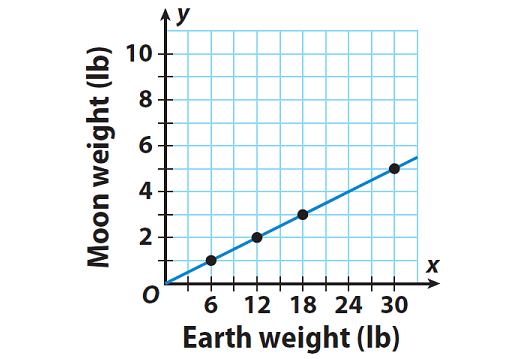
Solution :

Step 1 :

The graph of the given relationship contains the origin or the line is passing through the origin.

So,  the relationship is proportional.

Step 2 :

Make a table relating the weight of the object on the Moon and its weight on Earth.

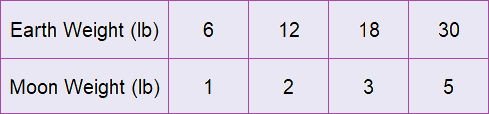
Step 3 :

Find the constant of proportionality.

Moon weight : Earth weight

1 : 6 = 1  : 6

2 : 12 = 1  : 6

3 : 18 = 1  : 6

5 : 30 = 1  : 6

The constant of proportionality is 1 : 6 or 1/6.

Step 4 :

Write an equation.

Let x represent weight on Earth.

Let y represent weight on the Moon.

The equation is y = kx.

Replace k with 1/6 in the above equation.

y = (1/6)x

y = x/6

Example 2 :

The entrance fee for Mountain World theme park is $20. Visitors purchase additional $2 tickets for rides, games, and food. The equation y = 2x + 20 gives the total cost, y, to visit the park, including purchasing x tickets. Explain  why the relationship between number of tickets and total cost is not proportional using a graph.

Solution :

Step 1 :

Choose several values for x that make sense in context.

Step 2 :

Plot the ordered pairs from the table. Describe the shape of the graph.

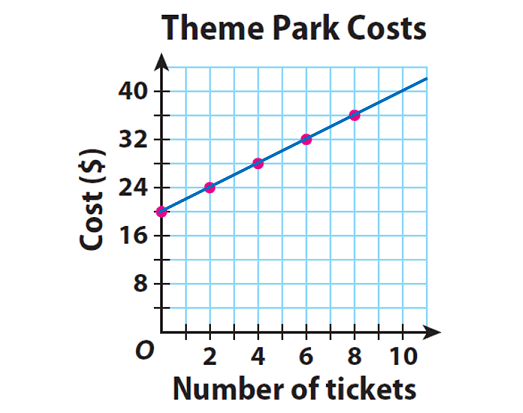
Step 3 :

In the above graph, the points lie on a line. But the line does not pass through the origin. So, the relationship between number of tickets and total cost is not proportional.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.