PROVE THAT PROBLEMS USING COMPOUND ANGLES FORMULA

Problem 1 :

Prove that (i) cos(30° + x)  =  (√3 cos x − sin x)/2

(ii) cos(π + θ) = −cos θ

(iii) sin(π + θ) = −sin θ.

Solution :

(i) cos(30° + x) :

cos (A + B)  =  cos A cos B - sin A sin B

cos(30° + x)  =  cos 30 cos x - sin 30 sin x

  =  (√3/2) cos x - (1/2) sin x

  =  (√3 cos x - sin x)/2

(ii) cos(π + θ) :

(π + θ) lies in the 3rd quadrant 

In third quadrant, we will have negative sign for all trigonometric ratios other than tan θ and cot θ. Here we have cos θ.

So, cos(π + θ)  =  -cos θ

(iii) sin(π + θ) = −sin θ :

(π + θ) lies in the 3rd quadrant 

In third quadrant, we will have negative sign for all trigonometric ratios other than tan θ and cot θ. Here we have sin θ.

So, sin(π + θ)  =  -sin θ

Problem 2 :

Find a quadratic equation whose roots are sin 15° and cos 15°.

Solution :

Since the roots of the required quadratic equation are sin 15° and cos 15°.

let α  =  sin 15° and β  = cos 15°

α  =  sin 15°  =  sin (45 - 30)

sin (A - B)  =  sin A cos B - cos A sin B

  =  sin 45 cos 30 - cos 45 sin 30

  =  (1/√2) (√3/2) - (1/√2) (1/2)

  =  (√3/2√2) - (1/2√2)

α = sin 15°  =  (√3 - 1)/2√2  ---(1)

α  =  cos 15°  =  cos (45 - 30)

cos (A - B)  =  cos A cos B + sin A sin B

  =  cos 45 cos 30 + sin 45 sin 30

  =  (1/√2) (√3/2) + (1/√2) (1/2)

  =  (√3/2√2) + (1/2√2)

β = cos 15°  =  (√3 + 1)/2√2  ---(2)

α + β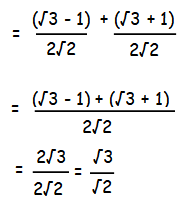

αβ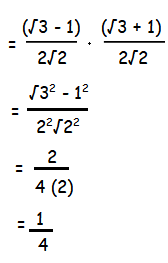

General form of quadratic equation

x² + (α + β)x + α β  =  0

x² + (√3/√2)x + (1/4)  =  0

4x²+ 2√3x + 1  =  0 

Problem 3 :

Use the compound-angle identities to simplify each of these expressions to one term: 

a)  cos 23° cos 22° - sin 23° sin 22°

Solution :

cos 23° cos 22° - sin 23° sin 22°

cos A cos B - sin A sin B = cos (A + B)

Using the above formula, we get

= cos (A + B)

= cos (23 + 22)

= cos 45

= √2/2

b) 1 - 2sin 45° cos 45°

Solution :

= 1 - 2sin 45° cos 45°

This problem can be done in two ways:

i) Using algebraic identity

ii) applying the values directly.

Method 1 :

= 1 - 2sin 45° cos 45°

= sin²45 + cos² 45 - 2sin 45° cos 45°

a² + b² - 2ab = (a - b)²

= (sin 45 - cos 45)²

= (√2/2 - √2/2)² 

= 0

Method 2 :

= 1 - 2sin 45° cos 45°

= 1 - 2√2/2 (√2/2)

= 1 - 2/2

= 1 - 1

= 0

Problem 4 :

sin (d + 45) - cos (d + 45) = √2 sin d

Solution :

L.H.S

= sin (d + 45) - cos (d + 45)

= (sin d cos 45 + cos d sin 45) - (cos d cos 45 - sin d sin 45)

= sin d cos 45 + cos d sin 45 - cos d cos 45 + sin d sin 45

= sin d (√2/2) + cos d (√2/2) - cos d (√2/2) + sin d (√2/2)

= (√2sin d/2) + (√2cos d/2) - (√2cos d/2) + (√2 sin d/2)

= (√2sin d + √2cos d - √2cos d + √2 sin d) / 2

= (2√2sin d) / 2

= √2sin d

R.H.S

Hence it is proved

Problem 5 :

[sin (45 + b + 30) cos (60 + b)]/sin 2b = (1/2) cosec b

Solution :

[sin (b + 30) cos (60 + b)]/sin 2b = (1/2) cosec b

sin (b + 30) = sin b cos 30 + cos b sin 30

= sin b (√3/2) + cos b (1/2)

= (√3 sin b + cos b)/2

cos (60 + b) = cos 60 cos b - sin 60 sin b

= (1/2) cos b - (√3/2) sin b

= (cos b - √3 sin b)/2

[sin (b + 30) cos (60 + b)]

= [(√3 sin b + cos b)/2] [(cos b - √3 sin b)/2]

= (cos b + √3 sin b)(cos b - √3 sin b)/4

= (cos² b - 3sin² b)/4

[sin (b + 30) cos (60 + b)]/sin 2b = (cos² b - 3sin² b)/4sin 2b

Problem 6 :

If tan x = 5/6 and tan y = 1/11, prove that x + y = π/4

Solution :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.