PROVE THAT THE LENGTH OF LATUS RECTUM OF THE HYPERBOLA

Question  1 :

Prove that the length of the latus rectum of the hyperbola (x²/a²) - (y²/b²)  =  1 is 2b²/a.

Solution :

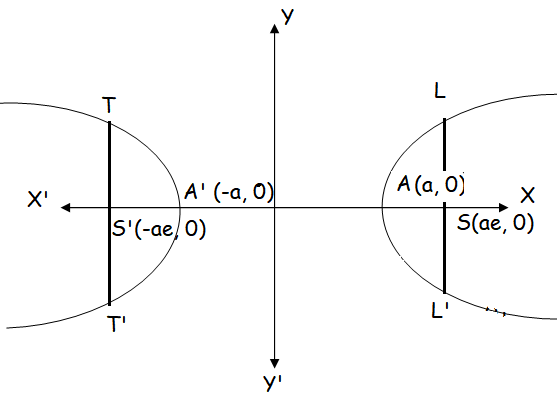
In the picture given above LSL' is the latus rectum and LS is called semi latus rectum TS'T' is also a latus rectum.

The coordinates of L are (ae, SL)

As L lies on the hyperbola.

(x²/a²) - (y²/b²)  =  1

The coordinate will satisfy the equation of the hyperbola

((ae)²/a²) - ((SL)²/b²)  =  1

(a²e²/a²) - ((SL)²/b²)  =  1

e² - 1  =  ((SL)²/b²)

(SL)²  =  b²(e² - 1)  -----(1)

b²  =  a² (e² - 1)

(e² - 1)  =  b²/a²

By applying the value of (e² - 1) in (1), we get 

(SL)²  =  b²(b²/a²) 

(SL)²  =  b⁴/a² 

SL  =  b²/a (length of semi latus rectum)

SL + SL'  =  2b²/a

Hence proved.

Question 2 :

Show that the absolute value of difference of the focal distances of any point P on the hyperbola is the length of its transverse axis

Solution :

Let p(x,y) be any point on the hyperbola

(x²/a²) - (y²/b²)  =  1.a

Let MPM' be the perpendicular through P on directrices ZK and Z'K'. Now by definition we get,

SP = e ∙ PM

SP = e ∙ NK

SP = e (CN - CK)

SP = e(X - (a/e))

SP = eX - a

and

S'P = e ∙ PM'

⇒ S'P = e ∙ (NK')

⇒ S'P = e (CK' + CN)

⇒ S'P = e(X + (a/e))

S'P = eX + a

Therefore,

S'P - SP = (a + ex) - (ex - a)

  =  a + ex - ex + a

  =  2a

= length of transverse axis.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.