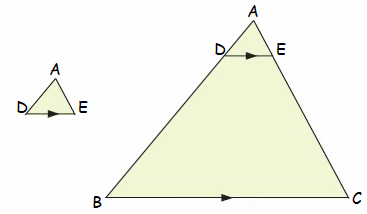
PROVE THE GIVEN TRIANGLES ARE SIMILAR USING AA SIMILARITY THEOREM

Prove that the given triangles are similar using AA theorem :

Example 1 :

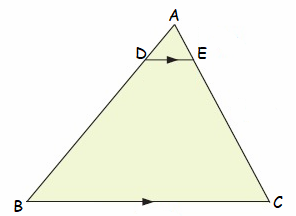
Solution :

Given :

DE || BC

To Prove :

∆ADE ~ ∆ABC

Proof :

In ∆ADE and ∆ABC

<ADE  =  <ABC

<AEC  =  <ACB

(corresponding angles are congruent)

So, ∆ADE and ∆ABC are similar.

Example 2 :

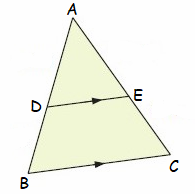
Solution :

Given :

DE || BC

To Prove :

∆ADE ~ ∆ABC

Proof :

In ∆ADE and ∆ABC

<ADE  =  <ABC

<AEC  =  <ACB

(corresponding angles are congruent)

So, ∆ADE and ∆ABC are similar.

Example 3  :

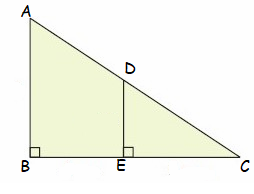
Solution :

Given :

DE || AB

To Prove :

∆DEC ~ ∆ABC

Proof :

In ∆DEC and ∆ABC

<DEC  =  <ABC  (90 degree)

<DCE  =  <ACB  (common)

So, ∆DEC and ∆ABC are similar.

Example 4  :

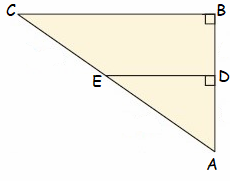
Solution :

Given :

DE || BC

To Prove :

∆ADE ~ ∆ABC

Proof :

In ∆ADE and ∆ABC

<ADE  =  <ABC

<EAD  =  <CAB

So, ∆ADE and ∆ABC are similar.

Example 5  :

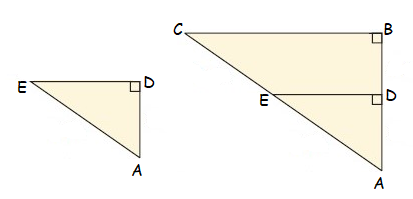
Solution :

Given :

AB || DE

To Prove :

∆ABC ~ ∆DEC

Proof :

In ∆ABC and ∆DEC

<ABC  =  <DEC (90 degree)

<ACB  =  <ECD (vertically opposite angles)

So, ∆ABC and ∆DEC are similar.

Hence, it is proved.

Example 6  :

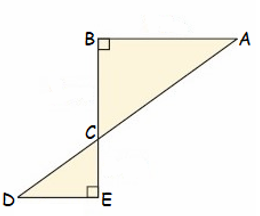
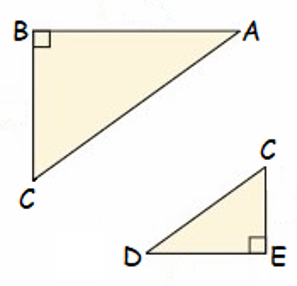
Given :

AB || DE

To Prove :

∆ABC ~ ∆DEC

Proof :

In ∆ABC and ∆DEC

<ABC  =  <DEC  (90 degree)

<DCE  =  <BCA  (vertically opposite angles)

So, ∆ABC and ∆DEC are similar.

Example 7  :

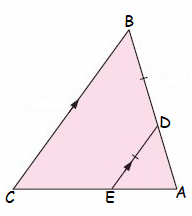
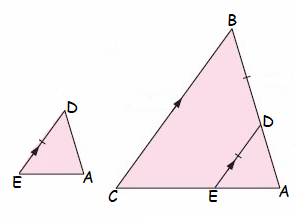
Given :

DE || BC

To Prove :

∆ADE ~ ∆ABC

Proof :

In ∆ADE and ∆ABC

<ADE  =  <ABC

<EAD  =  <CAB

So, ∆ADE and ∆ABC are similar.

Example 8  :

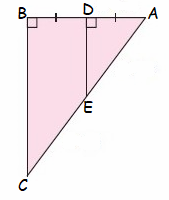
Solution :

Given :

DE || BC

To Prove :

∆ADE ~ ∆ABC

Proof :

In ∆ADE and ∆ABC

<ADE  =  <ABC (90 degree)

<DAE  =  <BAC (common)

So, ∆ADE and ∆ABC are similar.

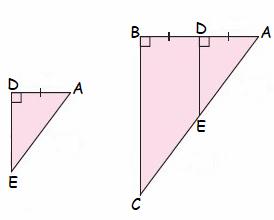
Example 9  :

Solution :

Given :

DE || AB

To Prove :

∆DEC ~ ∆ABC

Proof :

In ∆DEC and ∆ABC

<DEC  =  <ABC  (90 degree)

<DCE  =  <ABC  (common)

So, ∆DEC and ∆ABC are similar.

Explain how you know whether the triangles are similar. If possible, find the indicated length

Example 10 :

Find AC

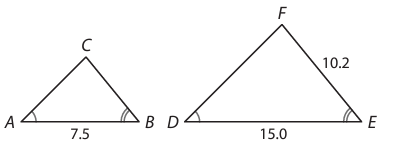
Solution :

<CAB = <FDE

<CBA = <FED

Using AA triangles ABC and DEF are similar.

BC/EF = AC/FD = AB/DE

BC/10.2 = AC/FD = 7.5/15

BC/10.2 = 7.5/15

BC = (7.5/15)(10.2)

BC = 5.1

AC/FD = 7.5/15

From the given information, AC is not possible to find.

Example 11 :

A flag pole casts a shadow that is 50 feet long. At the same time, a woman standing nearby who is 5 feet 4 inches tall casts a shadow that is 40 inches long. How tall is the flag pole to the nearest foot?

Solution :

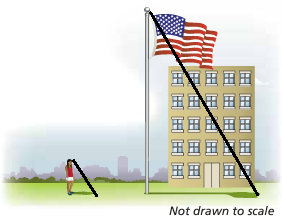
The triangles are similar.

Height of women = 5 feet 4 inches

1 feet = 12 inches

5 feet = 60 inches

5 feet 4 inches = 60 + 4 ==> 64 inches

height of women / height of flag pole = length of shadow of women / length of shadow of flag pole

Let x be the height of flagpole.

64/x = 40/50

64(50) = 40x

x = 3200/40

x = 80 feet.

So, height of flag pole is 80 feet.

Example 12 :

The shaded area is to be an industrial zone. Find the area of the industrial zone. Assume that King and Queen are parallel and that all streets and the track are straight.

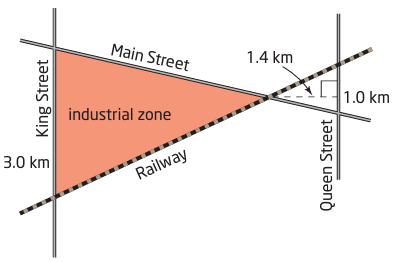
Solution :

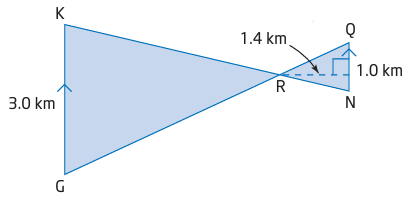
KG and QN are parallel. 

<KRG = <QRN

<GKR = <QNR

<KGR = <RQN

The triangles are similar. Since the triangles are similar, the corresponding sides will be in the same ratio.

KG/QN = 3/1

Corresponding sides be a and b. a : b = 3 : 1

Area will be in the ratio 3² : 1²

Area of large triangle = 1/2 x base x height

= (1/2) x 3 x height

= 1.5(height)

Area of small triangle = 1/2 x 1 x 1.4

= 0.7

1.5(height) / 0.7 = 9/1

1.5(height) = 9(0.7)

height = 9(0.7)/1.5

= 4.2

Applying 4.2 in 1.5 (height), we get 1.5(4.2) which is 6.3 cm².

So, the area of industrial region is 6.3 cm².

Example 13 :

a) Show why PQR is similar to STR.

b) Find the lengths x and y.

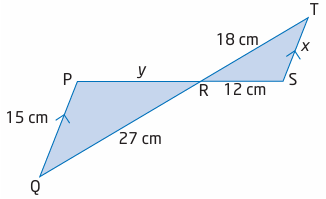
Solution :

<PRQ = <TRS (vertically opposite angles)

PQ and TS are parallel.

<PQR = <RTS (alternate interior angles)

Triangles PRQ and TRS are similar on AA. Comparing the ratio of corresponding sides.

PQ/TS = PR/RS = QR/TR

15/x = y/12 = 27/18

So, the required values of x and y are 10 and 18 respectively.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.